Le théorème de Thalès - L'univers des mathématiques

Le théorème de Thalès affirme que deux triangles semblables (des triangles qui possèdent les mêmes angles) sont des triangles proportionnels (les côtés de ces triangles forment un tableau de proportionnalité). Le tableau de proportionnalité doit contenir sur une même ligne les côtés d’un même triangle et sur une même colonne les côtés opposés aux angles égaux. Le mathématicien grec Thalès aurait utilisé ce théorème il y a plus de 2500 ans pour mesurer la hauteur d’une pyramide selon plusieurs récits antiques :

« Ainsi, vous, Thalès, le roi d’Égypte vous admire beaucoup, et, entre autres choses, il a été, au-delà de ce qu’on peut dire, ravi de la manière dont vous avez mesuré la pyramide sans le moindre embarras et sans avoir eu besoin d’aucun instrument. Après avoir dressé votre bâton à l’extrémité de l’ombre que projetait la pyramide, vous construisîtes deux triangles par la tangence d’un rayon, et vous démontrâtes qu’il y avait la même proportion entre la hauteur du bâton et la hauteur de la pyramide qu’entre la longueur des deux ombres. »
Le banquet des sept sages – Plutarque

Comment peut-on démontrer ce théorème simplement ? La démonstration la plus simple repose sur des considérations d’aires. Commençons par démontrer ce théorème dans le cas où les triangles semblables sont rectangles. On considère ainsi deux triangles rectangles semblables $OAB$ et $OA'B'$ puis on complète la figure en traçant plusieurs droites perpendiculaires comme ci-dessous :

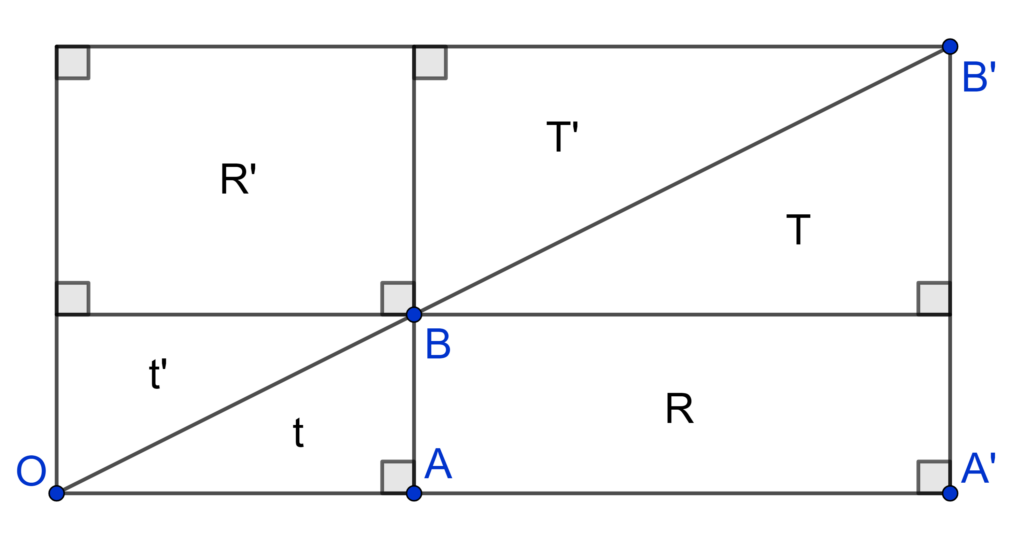
Les différentes aires délimitées dans la figure sont notées $t, t', R, R', T$ et $T'$ . On remarque par symétrie que $t=t'$ et $T= T'$ . On a aussi par symétrie $t+R+T=t'+R'+T$ puis en simplifiant cette dernière égalité on obtient $R = R'$ . Comme les deux aires rectangulaires $R$ et $R'$ sont identiques il vient :

$\displaystyle AB\times AA' = OA\times (A'B'-AB) \iff AB\times AA'=OA\times A'B'-OA\times AB \iff AB\times AA'+AB\times OA=OA\times A'B'\iff AB\times (OA+AA')=OA\times A'B'\iff AB\times OA'=OA\times A'B'\iff \frac{OA'}{OA}=\frac{A'B'}{AB}$

On peut à présent noter $k$ le rapport $OA'/OA=A'B'/AB$ puis utiliser le théorème de Pythagore pour obtenir :

$(OB')^2=(OA')^2+(A'B')^2=(k\times OA)^2+(k\times AB)^2=k^2\times OA^2+k^2\times AB^2=k^2\times (OA^2+AB^2)=k^2\times OB^2$

On déduit que $(OB'/OB)^2=k^2$ puis que $OB'/OB=k$ ce qui nous donne les égalités du théorème de Thalès :

$\displaystyle \frac{OA'}{OA}=\frac{OB'}{OB}=\frac{A'B'}{AB}$

Pourquoi le théorème de Thalès reste-t-il valable même si les deux triangles semblables $OAB$ et $OA'B'$ ne sont pas rectangles ? Dans le cas général, on peut en effet considérer les hauteurs de ces triangles comme dans la figure ci-dessous :

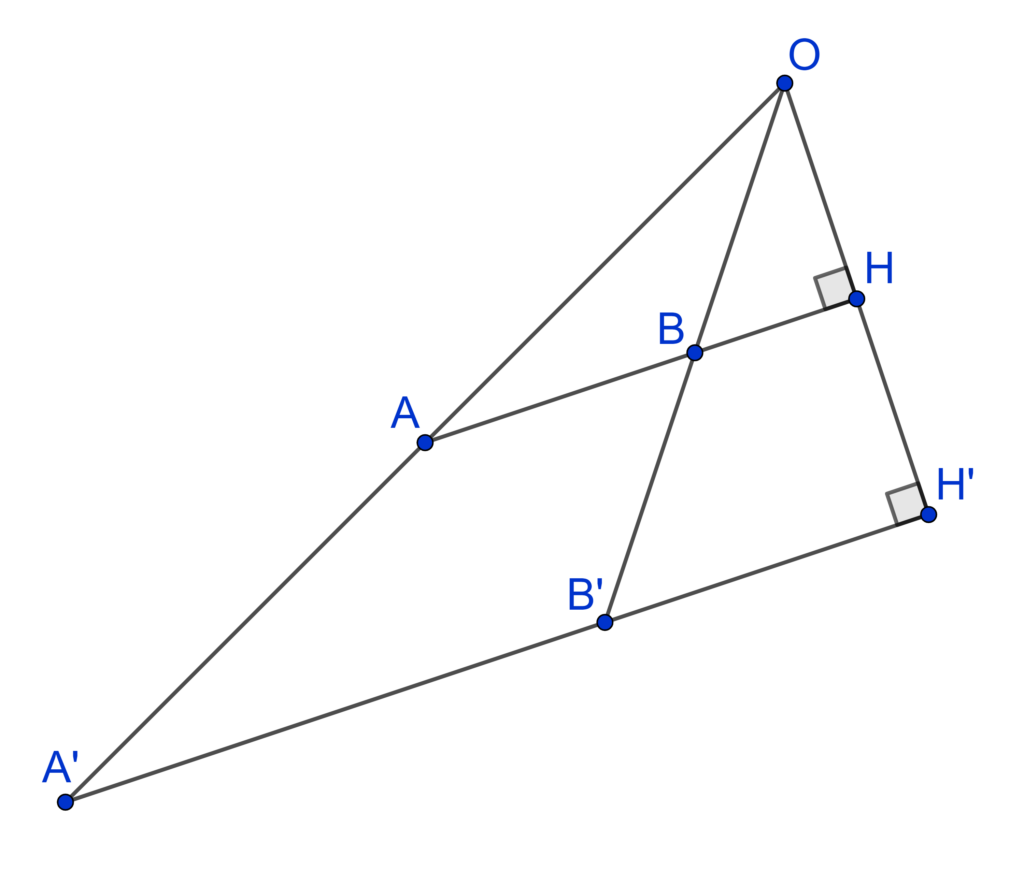
Les triangles $OAH$ et $OA'H'$ sont rectangles et semblables donc on a $OH'/OH=OA'/OA=A'H'/AH$ . De plus les triangles $OBH$ et $OB'H'$ sont rectangles et semblables donc on a $OH'/OH=OB'/OB=B'H'/BH$ . Si on note à nouveau $k$ le rapport $OH'/OH$ alors il est clair que $OA'/OA=OB'/OB=k$ . D’autre part les égalités $A'H'=k\times AH$ et $B'H'=k\times BH$ nous donnent par soustraction $A'H'-B'H'=k\times (AH-BH)$ donc $A'B'=k\times AB$ ainsi on obtient une fois de plus les égalités de Thalès :

$\displaystyle \frac{OA'}{OA}=\frac{OB'}{OB}=\frac{A'B'}{AB}$

Une dernière remarque : la soustraction des égalités $A'H'=k\times AH$ et $B'H'=k\times BH$ nous permet en fait de conclure seulement dans le cas où l’angle $\widehat{AOB}$ est aigu comme sur la figure considérée mais si cet angle était obtus il suffirait alors d’additionner ces égalités.

Partager :

Laisser un commentaire Annuler la réponse