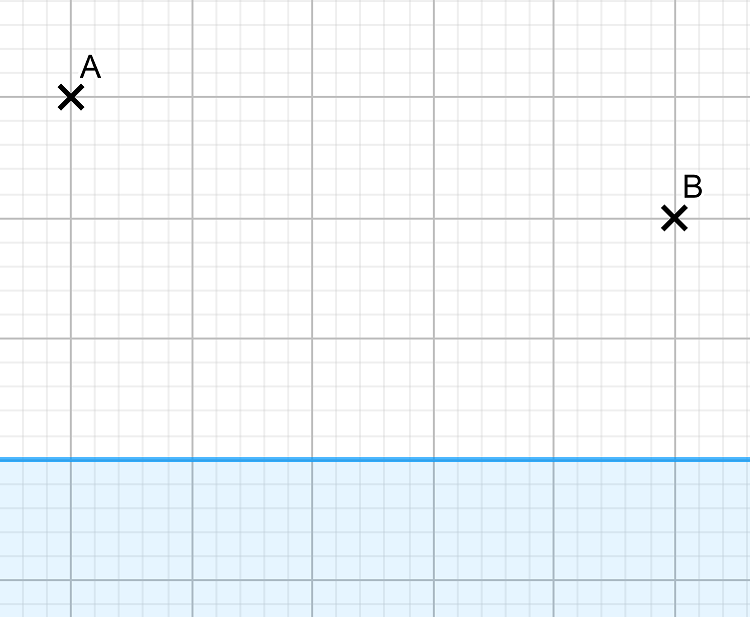
Deux maisons se trouvent du même côté d’une rivière. On représente ces maisons sur une carte par deux points A et B. Une personne qui se trouve à la maison A souhaite se rendre à la maison B tout en effectuant un arrêt sur son trajet au bord de la rivière. Quel est le chemin le plus court ?
Voici une représentation possible de la situation (le quadrillage peut être une aide mais il n’est pas nécessaire dans la résolution) :
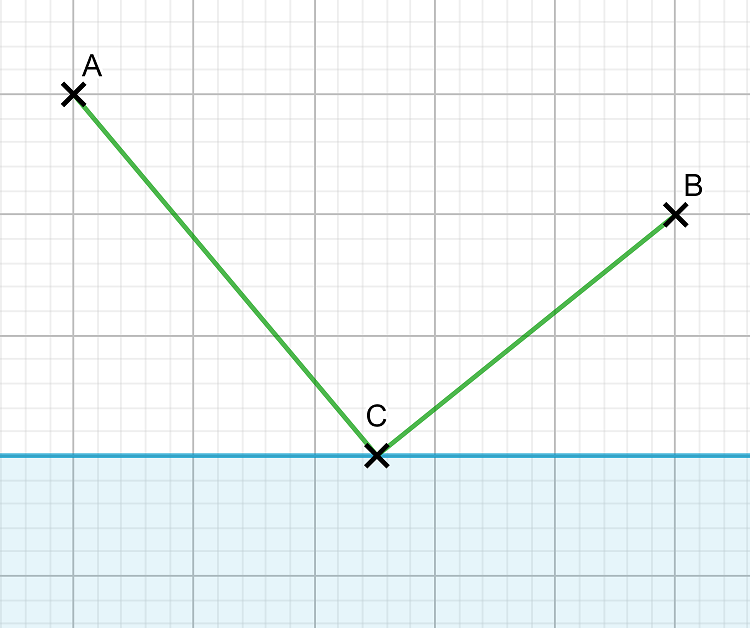
Voici un exemple de trajet possible mais il y a plus rapide, ce n’est donc pas la solution :
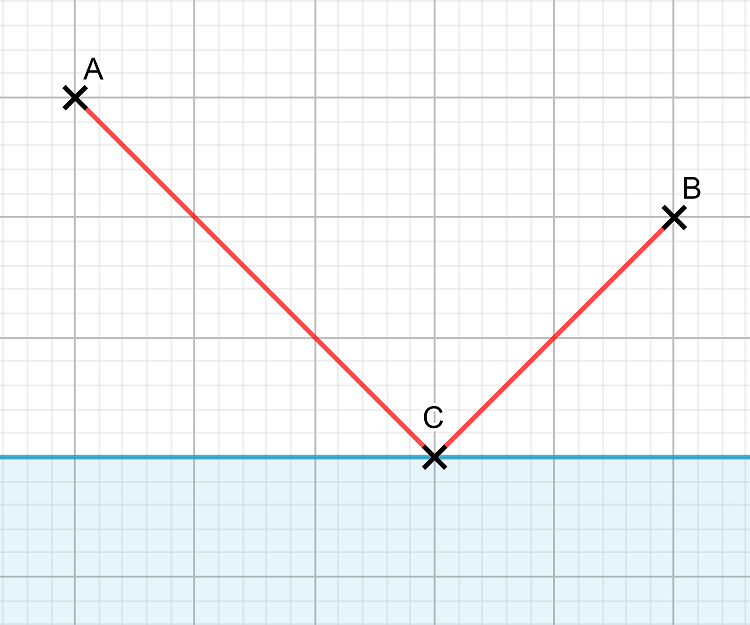
Comment peut-on arriver à cette conclusion ? L’astuce est de considérer B’ le symétrique du point B par rapport à la droite bleue. Le point C solution du problème est alors le point d’intersection de la droite bleue avec la droite (AB’).
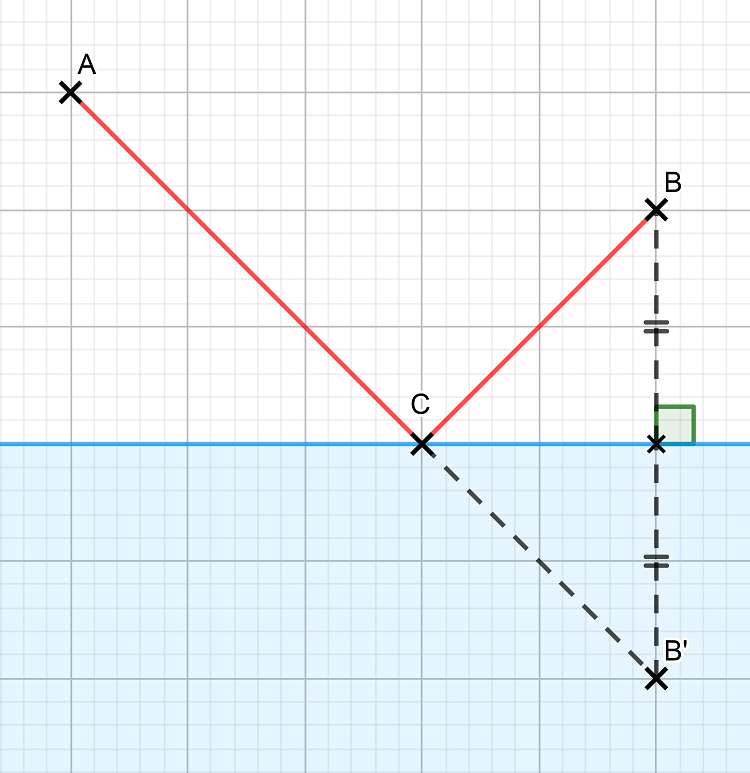
En effet, la symétrie axiale conserve les distances donc on a AC+CB=AC+CB’. Si l’on recherche un point C qui minimise la longueur AC+CB cela revient à chercher aussi un point C qui minimise la longueur AC+CB’. Le trajet le plus court de A vers B’ est clairement la droite (AB’) donc le point C qui permet de minimiser AC+CB’ est sur la droite (AB’).