Vous utilisez certainement chez vous de l’énergie qui arrive dans votre foyer par un courant électrique possédant une certaine intensité et une certaine tension. Cet article a pour but de vous donner une notion intuitive de ce que représente l’intensité et la tension d’un courant électrique mais aussi d’aborder une question plus générale : qu’est ce que l’énergie ? C’est un sujet complexe qui se trouve à la frontière des mathématiques. On peut toutefois, comme en mathématiques, poser quelques définitions et admettre quelques principes simples puis voir où tout cela nous mène. On va partir ici de l’idée que l’énergie est simplement la capacité à déplacer de la matière. Lorsque nous soulevons par exemple une bouteille d’eau de 1 L posée par terre à 1 dm au dessus du sol (on rappelle que 1 m = 10 dm), nous sentons bien que nous utilisons une certaine quantité de notre énergie : convenons d’appeler cette quantité d’énergie le Joule. Le Joule que l’on note simplement J est en effet l’unité de mesure de l’énergie et il se trouve qu’un bon ordre de grandeur du Joule peut être représenté par cette action.
Quelle quantité d’énergie faut-il pour soulever 4 L d’eau à 1 dm au dessus du sol ? Il paraît assez logique de supposer que l’énergie est proportionnelle à la quantité d’eau soulevée ainsi il faut 4 Joules. Quelle quantité d’énergie faut-il pour soulever 4 L d’eau à 1 m au dessus du sol ? Il est à nouveau assez naturel de supposer que la quantité d’énergie est proportionnelle à la hauteur et de conclure qu’il nous faudra cette fois 40 Joules. On obtient ainsi une formule pour calculer l’énergie 
Peut-on stocker et transporter cette énergie ? Supposons que l’on dispose d’une balance avec deux plateaux et que le mécanisme de la balance puisse être bloqué. Le premier plateau se trouve à 1 m au dessus du sol et le second plateau est sur le sol. En bas du premier plateau se trouvent 4 L d’eau dans un seau. Une personne soulève le seau de 4 L d’eau pour le mettre sur le premier plateau mais la balance ne bouge pas car son mécanisme est bloqué. L’énergie dépensée par cette personne est de 40 Joules. La balance bloquée nous permet de stocker cette énergie et de la transporter. En effet, si un peu plus tard sur le second plateau on dispose un seau de 3 L d’eau et que l’on débloque le mécanisme de la balance alors le second plateau s’élèvera à 1 m de haut tandis que le premier plateau descendra au niveau du sol. Nous avons donc stocké 40 Joules puis transporté une partie de cette énergie et finalement récupéré 30 Joules. Il faut obligatoirement mettre moins d’eau sur le second plateau ainsi transporter de l’énergie entraine une perte.
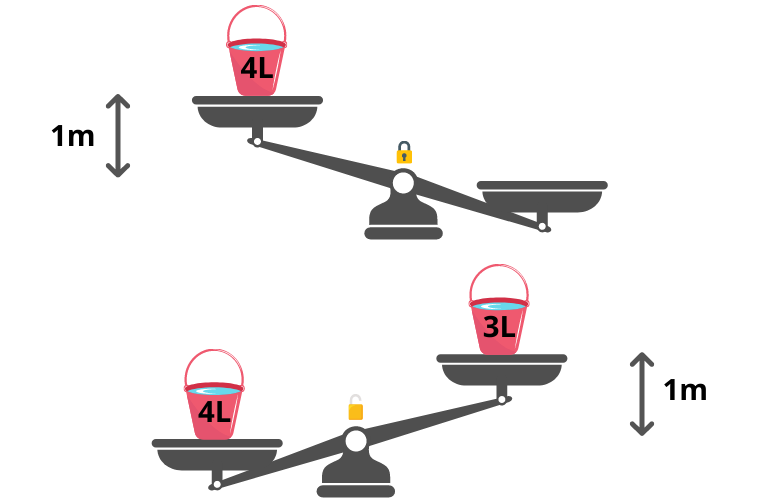
La balance n’est pas très pratique pour transporter l’énergie sur de plus grandes distances. Nous pouvons toutefois améliorer notre système. Lorsque le seau contenant 3 L d’eau s’élève sur le second plateau à 1 m de haut on ouvre un petit robinet au fond du seau raccordé à un tuyau. Nous pouvons à présent transporter nos 3 L d’eau avec ce tuyau jusqu’à un village se trouvant beaucoup plus loin en contrebas. L’eau qui sort du tuyau peut servir à entrainer une hélice et des poulies pour tirer ou soulever une charge. Cette eau peut nous permettre de déplacer de la matière : il s’agit bien d’une forme d’énergie.
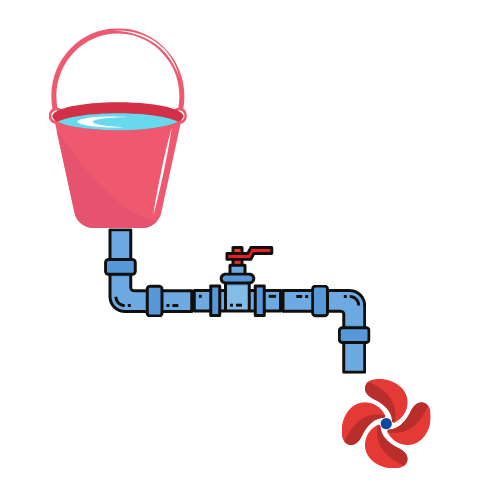
Nous avons trouvé des moyens de stocker et transporter de l’énergie mais la production de cette énergie repose pour l’instant sur une personne qui doit porter des seaux de 4 L d’eau sur un plateau à 1 m de haut. Nous voulons à présent aller plus loin et récupérer une énergie qui ne serait pas produite par un humain. Au village, on décide de poser sur le toit d’une maison à 5 m de haut une cuve pouvant contenir 100 L d’eau. Il y a également un robinet au fond de la cuve raccordé à un tuyau. Pendant la saison des pluies, la cuve s’est remplie. De quelle quantité d’énergie dispose-t-on alors dans le village ?
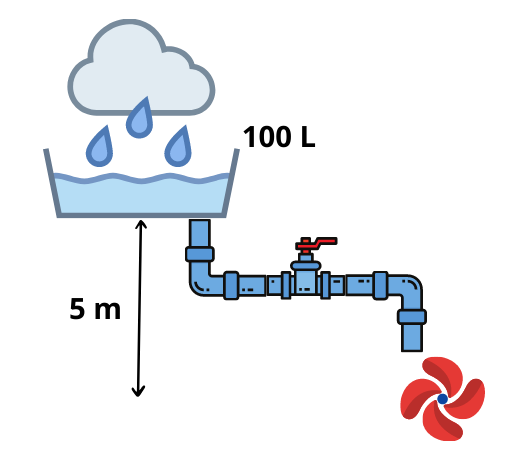
Pour calculer cette énergie, il faut la mesurer avec notre unité de mesure choisie le Joule. On rappelle que 10 Joules correspond à soulever 1 L d’eau à 1 m de haut. On peut être tenté de calculer la quantité d’énergie de la cuve en l’utilisant pour remplir des seaux sur une balance et en comptant le nombre de fois où l’on soulève 1 L d’eau à 1 m de haut mais cette méthode n’est pas très pratique et elle gaspille de l’énergie. Il y a plus simple : on imagine une très grande balance qui contiendrait sur l’un de ses plateaux la cuve à 50 dm de haut, avec cette balance on constate qu’il est alors possible de soulever une cuve quasiment identique sur le second plateau à 50 dm de haut. Ainsi la quantité d’énergie que l’on peut récupérer avec la cuve est au maximum de 
On place à présent une hélice au bout du tuyau raccordé à la cuve. La vitesse de l’hélice augmente lorsque l’hélice reçoit plus rapidement l’énergie de la cuve. Il est donc intéressant de pouvoir mesurer notre vitesse de production d’énergie. Si notre système est capable de produire 1 Joule d’énergie à chaque seconde alors on dira que sa puissance est de 1 Watt. Le Watt se note W et on a ainsi par définition 1 W = 1 J/s. Pour contrôler la puissance de notre système, il faut contrôler la quantité d’eau qui s’écoule par notre tuyau c’est à dire le débit d’eau que l’on peut mesurer par exemple en L/s. Si le tuyau raccordé à notre cuve permet de remplir une bouteille de 1 L en 10 secondes alors chaque litre de cette eau qui se trouvait à 50 dm de haut arrive au bout du tuyau avec une énergie de 50 J : la puissance de notre système sera de 50 joules toutes les 10 secondes donc de 50/10 = 5 W. Cet exemple nous montre que la puissance d’un tel dispositif est en fait calculée avec 
La finalité de notre système est d’entrainer une hélice avec un tuyau d’eau mais dans la nature nous pouvons trouver des cascades. On souhaite maintenant mettre notre hélice directement sous une cascade mais comment faut-il choisir cette cascade ? L’étude de la cuve du village nous montre qu’il faut nous intéresser à la hauteur de la cascade 
De nos jours, l’énergie est principalement transportée par l’électricité et pour comprendre sa nature il peut être utile de se rattacher aux exemples précédents. Le transport de l’énergie dans ces exemples reposait sur le transport de l’eau. Pour l’électricité, il y a de même un transport de matière car des particules de matière appelés électrons se déplacent à l’intérieur des câbles électriques. On peut utiliser une analogie avec la cascade pour comprendre la nature d’un courant électrique de tension 
Note : La définition du Joule utilisée dans cet article repose sur une approximation (en réalité les conventions adoptées pour nos unités de mesure nous permettent de conclure que l’énergie utilisée pour soulever 1 L d’eau à 1 dm de haut n’est pas 10 J mais environ 9,81 J). L’énergie thermique peut aussi rentrer dans le cadre de la définition de cet article car il s’agit bien d’un déplacement de matière mais à l’échelle microscopique.