Vous participez à un jeu où l’on vous demande de choisir entre trois portes. L’une de ces portes cache dans une pièce un trésor tandis que les deux autres mènent simplement à des pièces vides. Le maître du jeu qui sait où se trouve le trésor vous demande de choisir une porte, toutefois après que vous ayez choisi une porte, celui-ci ouvre une autre porte menant à une pièce vide et vous propose une dernière possibilité : maintenir votre choix ou bien changer de porte. Qu’est-il préférable de faire ?
Indice
On peut penser que le choix final importe peu et qu’il est aussi judicieux de maintenir son choix que de changer de porte. C’est pourtant faux et il y a bien un choix final préférable.
Solution
On donne des noms aux portes, la porte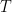 
désigne la porte qui cache le trésor tandis que les portes qui mènent à des pièces vides sont appelées 
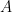et 
. Il y a alors trois possibilités dans le jeu :
– Le joueur choisit la porte : dans ce cas le maître du jeu ouvre une porte qui mène à une pièce vide et la porte restante ne contient pas le trésor.
– Le joueur choisit la porte : dans ce cas le maître du jeu ouvre la porte et la porte restante contient le trésor.
– Le joueur choisit la porte : dans ce cas le maître du jeu ouvre la porte et la porte restante contient le trésor.
Chacune des trois possibilités a autant de chances de se réaliser que les autres. On peut observer toutefois que dans 2 cas sur 3 c’est la porte restante qui contient le trésor. En conclusion il est préférable de changer de porte lors de son choix final.
désigne la porte qui cache le trésor tandis que les portes qui mènent à des pièces vides sont appelées et 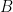. Il y a alors trois possibilités dans le jeu :– Le joueur choisit la porte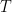
: dans ce cas le maître du jeu ouvre une porte qui mène à une pièce vide et la porte restante ne contient pas le trésor.– Le joueur choisit la porte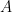
: dans ce cas le maître du jeu ouvre la porte 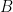et la porte restante contient le trésor.– Le joueur choisit la porte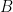
: dans ce cas le maître du jeu ouvre la porte 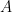et la porte restante contient le trésor.Chacune des trois possibilités a autant de chances de se réaliser que les autres. On peut observer toutefois que dans 2 cas sur 3 c’est la porte restante qui contient le trésor. En conclusion il est préférable de changer de porte lors de son choix final.
Approfondissement
La solution précédente a le mérite d’être facile à comprendre, toutefois elle risque de ne pas satisfaire ceux qui se demandent comment modéliser le problème mathématiquement. On peut prendre comme espace probabilisé l’ensemble 
muni de sa tribu constituée de l’ensemble des parties de 
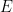et de la probabilité 
(probabilité usuelle du dénombrement qui consiste à diviser les cardinaux). Un évènement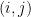 
de 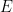sera traduit par « Le joueur a choisi la porte 
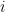et le trésor se trouve derrière la porte 
« . Le problème consiste à déterminer s’il vaut mieux jouer avec la stratégie de changer de porte à la fin ou bien avec la stratégie de ne pas changer d’avis. Toutefois le choix de cette stratégie modifie la définition de l’évènement « Le joueur gagne » noté 
:
– Si la stratégie choisie est de changer de porte à la fin alors
donc la probabilité de est 
.
– Si la stratégie choisie est de ne pas changer d’avis alors
donc la probabilité de est 
.
On peut conclure qu’il est ainsi préférable de jouer au jeu avec la stratégie de changer de porte. Il est possible de vérifier cela avec la simulation informatique proposée dans le lien suivant : Simulation informatique. Dans cette énigme, le maître du jeu vous laisse en fait subtilement la possibilité de redéfinir la règle qui permet de gagner et on a tendance à interpréter sa proposition comme un piège, il faut pourtant saisir cette opportunité.
muni de sa tribu constituée de l’ensemble des parties de et de la probabilité (probabilité usuelle du dénombrement qui consiste à diviser les cardinaux). Un évènement de sera traduit par « Le joueur a choisi la porte et le trésor se trouve derrière la porte « . Le problème consiste à déterminer s’il vaut mieux jouer avec la stratégie de changer de porte à la fin ou bien avec la stratégie de ne pas changer d’avis. Toutefois le choix de cette stratégie modifie la définition de l’évènement « Le joueur gagne » noté :– Si la stratégie choisie est de changer de porte à la fin alors
donc la probabilité de est .– Si la stratégie choisie est de ne pas changer d’avis alors
donc la probabilité de est .On peut conclure qu’il est ainsi préférable de jouer au jeu avec la stratégie de changer de porte. Il est possible de vérifier cela avec la simulation informatique proposée dans le lien suivant : Simulation informatique. Dans cette énigme, le maître du jeu vous laisse en fait subtilement la possibilité de redéfinir la règle qui permet de gagner et on a tendance à interpréter sa proposition comme un piège, il faut pourtant saisir cette opportunité.