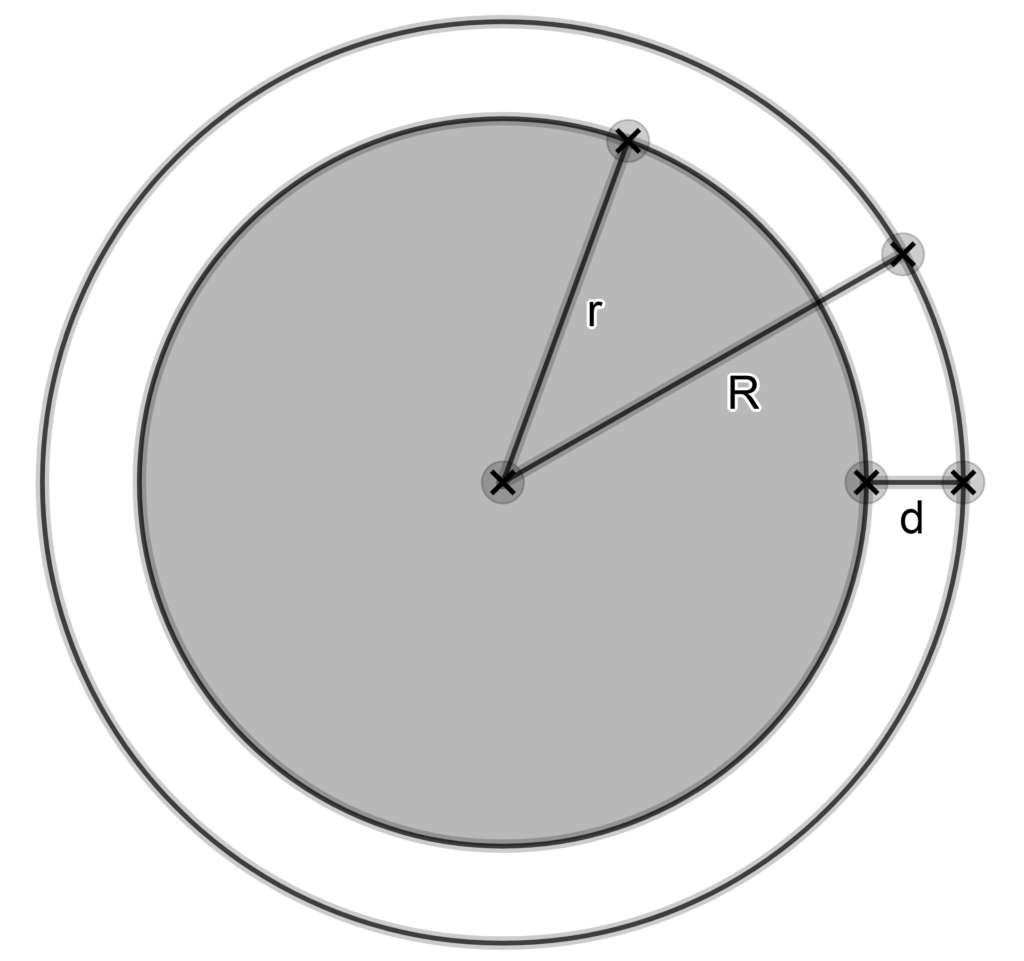
Imaginez une ficelle dont la longueur est égale au périmètre de la Terre. On rajoute 1 mètre de longueur à cette ficelle puis on la dispose dans un plan de manière à former un cercle et on place ensuite la Terre au centre de ce cercle. Quel est l’ordre de grandeur de la longueur qui sépare le cercle formé par la ficelle et le cercle formé par la Terre ? On pourra noter 
Indice
On peut penser par intuition que l’ordre de grandeur de la distance est très petit (inférieur au millimètre) mais cette distance mesure quand même environ 16 cm. Comment obtient-on ce résultat ?
est très petit (inférieur au millimètre) mais cette distance mesure quand même environ 16 cm. Comment obtient-on ce résultat ? Solution
Selon l’énoncé, la différence entre les deux périmètres, celui du cercle de la ficelle et celui de la Terre, est égale à 1 mètre. De plus, nous pouvons écrire en notant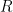 
le rayon du cercle de la ficelle et 
le rayon de la Terre que cette différence est aussi égale à 
. On obtient ainsi l’égalité 
qui nous donne la formule 
m. Ce qui est remarquable dans ce problème est que cette distance ne dépend pas du rayon de la Terre ni même de ce que l’on décide d’entourer ! Que l’on réalise l’expérience avec la Terre, Jupiter ou un ballon, le résultat restera le même : environ 16 cm.
le rayon du cercle de la ficelle et le rayon de la Terre que cette différence est aussi égale à . On obtient ainsi l’égalité qui nous donne la formule m. Ce qui est remarquable dans ce problème est que cette distance ne dépend pas du rayon de la Terre ni même de ce que l’on décide d’entourer ! Que l’on réalise l’expérience avec la Terre, Jupiter ou un ballon, le résultat restera le même : environ 16 cm.