Soixante personnes sont réunies dans une pièce, quelle est la probabilité qu’au moins deux personnes aient la même date d’anniversaire ?
Indice
Il est plus facile de calculer la probabilité de l’évènement contraire : la probabilité que toutes les personnes aient des dates d’anniversaire différentes. S’il y a seulement 2 personnes dans la pièce alors cette probabilité est 
car il y a 364 choix possibles parmi 365 pour une date d’anniversaire différente. Pour obtenir une valeur approchée de cette probabilité on peut en effet négliger la possibilité qu’une personne soit née un 29 février lors d’une année bissextile de 366 jours. Que se passe-t-il lorsqu’il y a plus de personnes dans la pièce ?
car il y a 364 choix possibles parmi 365 pour une date d’anniversaire différente. Pour obtenir une valeur approchée de cette probabilité on peut en effet négliger la possibilité qu’une personne soit née un 29 février lors d’une année bissextile de 366 jours. Que se passe-t-il lorsqu’il y a plus de personnes dans la pièce ? Solution
S’il y a 3 personnes dans la pièce alors pour que ces trois personnes n’aient pas la même date d’anniversaire il faut que les deux premières personnes aient des dates d’anniversaire différentes (la probabilité de cet évènement noté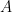 
est ) puis que la troisième personne ait une date d’anniversaire différente des deux premières personnes (la probabilité de ce dernier évènement sachant que est réalisé est 
). Par définition d’une probabilité conditionnelle on peut multiplier ces probabilités ainsi la probabilité que 3 personnes aient des dates d’anniversaire différentes est 
. A présent, il nous suffit de recommencer ce raisonnement plusieurs fois dans le cas d’une pièce réunissant 60 personnes et la probabilité que toutes les personnes aient des dates d’anniversaire différentes est donc 
. Finalement, la probabilité qu’au moins deux personnes aient la même date d’anniversaire dans une pièce regroupant 60 personnes est environ 
. Ce résultat peut paraître surprenant : vous pouvez affirmer avec une quasi-certitude que dans un groupe de 60 personnes il y a au moins deux personnes qui ont la même date d’anniversaire !
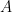est ) puis que la troisième personne ait une date d’anniversaire différente des deux premières personnes (la probabilité de ce dernier évènement sachant que est réalisé est ). Par définition d’une probabilité conditionnelle on peut multiplier ces probabilités ainsi la probabilité que 3 personnes aient des dates d’anniversaire différentes est . A présent, il nous suffit de recommencer ce raisonnement plusieurs fois dans le cas d’une pièce réunissant 60 personnes et la probabilité que toutes les personnes aient des dates d’anniversaire différentes est donc . Finalement, la probabilité qu’au moins deux personnes aient la même date d’anniversaire dans une pièce regroupant 60 personnes est environ . Ce résultat peut paraître surprenant : vous pouvez affirmer avec une quasi-certitude que dans un groupe de 60 personnes il y a au moins deux personnes qui ont la même date d’anniversaire ! Approfondissement
Comment peut-on trouver la solution exacte du problème en tenant compte des années bissextiles ? On peut modéliser le choix d’une date d’anniversaire en prenant pour univers l’ensemble 
muni de la probabilité 
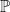telle que 
et 
(dans cette modélisation la date du 29 février est la date numérotée 366). S’il y a deux personnes dans la salle alors la probabilité que ces deux personnes n’aient pas la même date d’anniversaire est 
. De même s’il y a trois personnes dans la salle alors la probabilité que ces trois personnes aient des dates d’anniversaire différentes est 
. On peut continuer ces calculs pour une pièce regroupant 60 personnes et conclure que la probabilité qu’au moins deux personnes aient la même date d’anniversaire est 
. On constate que ce résultat est très proche de celui obtenu dans la modélisation simplifiée du problème.
muni de la probabilité telle que et (dans cette modélisation la date du 29 février est la date numérotée 366). S’il y a deux personnes dans la salle alors la probabilité que ces deux personnes n’aient pas la même date d’anniversaire est . De même s’il y a trois personnes dans la salle alors la probabilité que ces trois personnes aient des dates d’anniversaire différentes est . On peut continuer ces calculs pour une pièce regroupant 60 personnes et conclure que la probabilité qu’au moins deux personnes aient la même date d’anniversaire est . On constate que ce résultat est très proche de celui obtenu dans la modélisation simplifiée du problème.