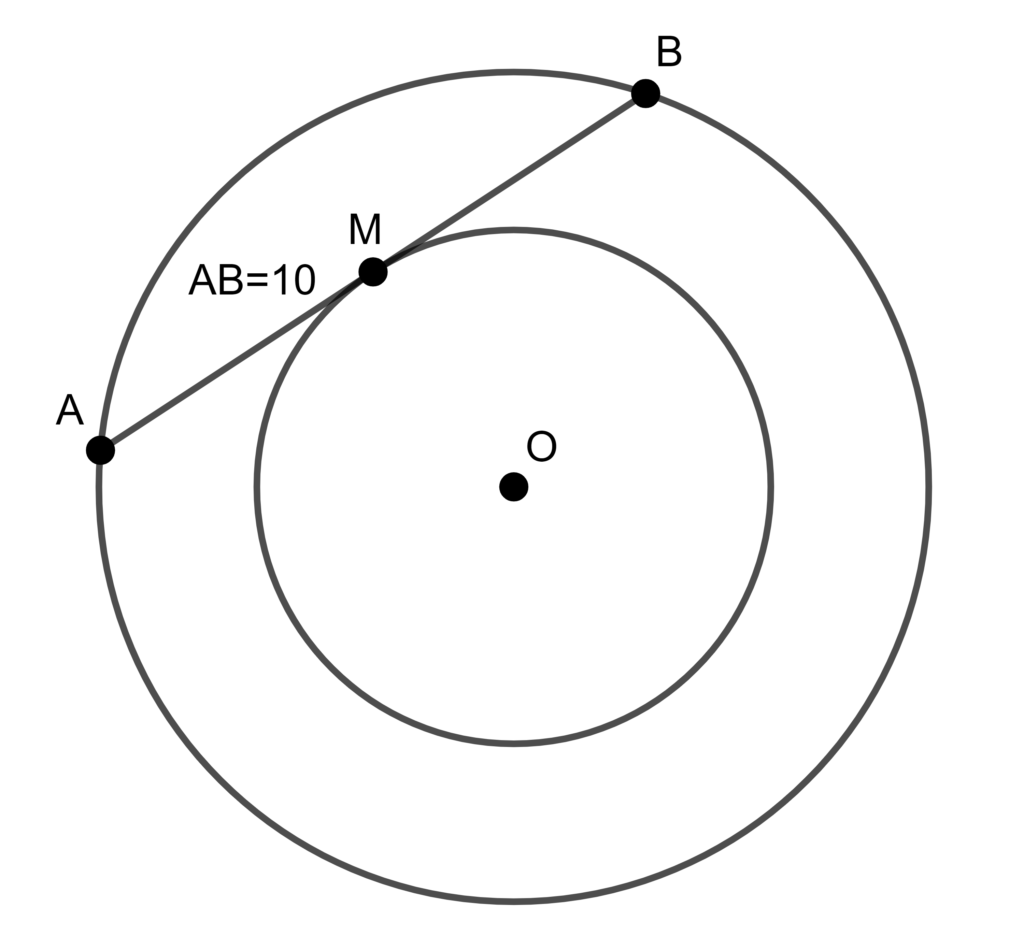
Le couloir circulaire - L'univers des mathématiques

Une bibliothèque de centre-ville possède une architecture originale : les livres sont rangés dans un cylindre central, accessible par un couloir circulaire. Une corde du grand cercle extérieur, tangente au cercle intérieur contenant les livres mesure 10 mètres. Quelle est l’aire du couloir ?

*Les deux cercles ont pour centre O et la corde [AB] est tangente en M au cercle intérieur.*

Indice

On note 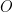$O$ le centre des deux cercles, $[AB]$ la corde de longueur $10$ et $M$ le point de tangence. Il est vain de rechercher les rayons (du cercle intérieur ou du cercle extérieur) car il y a une infinité de possibilités pour réaliser une figure dans la configuration du problème. Ce qui est surprenant c’est que l’aire du couloir circulaire que l’on demande de calculer ne dépend pas des valeurs de ces rayons !

Solution

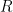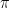On admet que $(OM)$ est la médiatrice de $[AB]$ . On note $r$ le rayon du petit cercle et $R$ le rayon du grand cercle. La longueur de la corde $[AB]$ est notée $c$ , d’après le théorème de Pythago re dans le triangle rectangle $AMO$ rectangle en $M$ on a $(c/2)^2+r^2=R^2$ , cette égalité est équivalente en multipliant des deux côtés par $\pi$ à l’égalité $\pi(R^2-r^2)=\pi(c/2)^2$ . L’aire du couloir est donc $c^2\pi/4$ ce qui nous donne pour $c=10$ mètres une aire de $25\pi$ mètres carrés.

Approfondissement

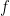On se propose de vérifier ce qui a été admis dans la solution précédente en montrant que la tangente à un cercle en un point $M$ est perpendiculaire au rayon issu de $M$ . Si on note $r$ le rayon du cercle alors la moitié de ce cercle correspond au graphique de la fonction $f:x\mapsto \sqrt{r^2-x^2}$ sur l’intervalle $]-r;r[$ . Le graphique de $f$ considéré est dans un repère orthonormé avec pour origine 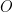$O$ le centre du cercle et pour axe des ordonnées $(OM)$ de sorte que $M$ a pour abscisse $0$ dans ce repère. 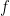La fonction $f$ est dérivable sur $]-r;r[$ avec $\forall x\in ]-r;r[,f'(x)=-x/\sqrt{r^2-x^2}$ . Le coefficient directeur de la tangente au cercle en $M$ est alors par définition le nombre dérivé $f'(0)=-0/r=0$ . Ceci prouve que la tangente est parallèle à l’axe des abscisses dans le repère donc perpendiculaire au rayon $[OM]$ .

Partager :

Laisser un commentaire Annuler la réponse