Le nombre Pi

Comment définir le nombre ? La définition classique de ce nombre qui est présentée à l’école est la suivante : dans n’importe quel cercle, le quotient de sa circonférence par son diamètre est toujours le même peu importe la taille du cercle, ce quotient est un nombre que l’on note et que l’on appelle Pi.

Mais comment peut-on démontrer que la division mentionnée précédemment donne bien toujours le même résultat peu importe la taille du cercle ? C’est ce que l’on se propose de démontrer dans cet article, ainsi notre définition de sera valide et complète. Nous allons utiliser pour cela des polygones réguliers : ce sont des polygones qui ont tous leurs côtés de la même longueur et tous leurs angles de la même mesure. Par exemple, le polygone régulier à trois côtés est un triangle équilatéral tandis que le polygone régulier à quatre côtés est un carré. Un polygone régulier est toujours inscrit dans un cercle et il ressemble de plus en plus à son cercle inscrit à mesure que son nombre de côtés augmente. Nous pouvons ainsi définir la circonférence d’un cercle comme la limite de la suite des périmètres des polygones réguliers inscrits dans ce cercle. On admet ici que cette suite croissante converge bien vers une limite définie comme la circonférence.

Considérons à présent deux cercles, un cercle orange de rayon et un cercle bleu de rayon qui n’ont à priori pas la même taille. Supposons pour simplifier que les deux cercles ont le même centre noté . L’idée est de considérer dans les deux cercles un polygone régulier inscrit à côtés, on note ce polygone pour le cercle orange de rayon et ce polygone pour le cercle bleu de rayon . On a représenté ci-dessous la situation dans le cas où ainsi les polygones réguliers et sont les pentagones réguliers et :

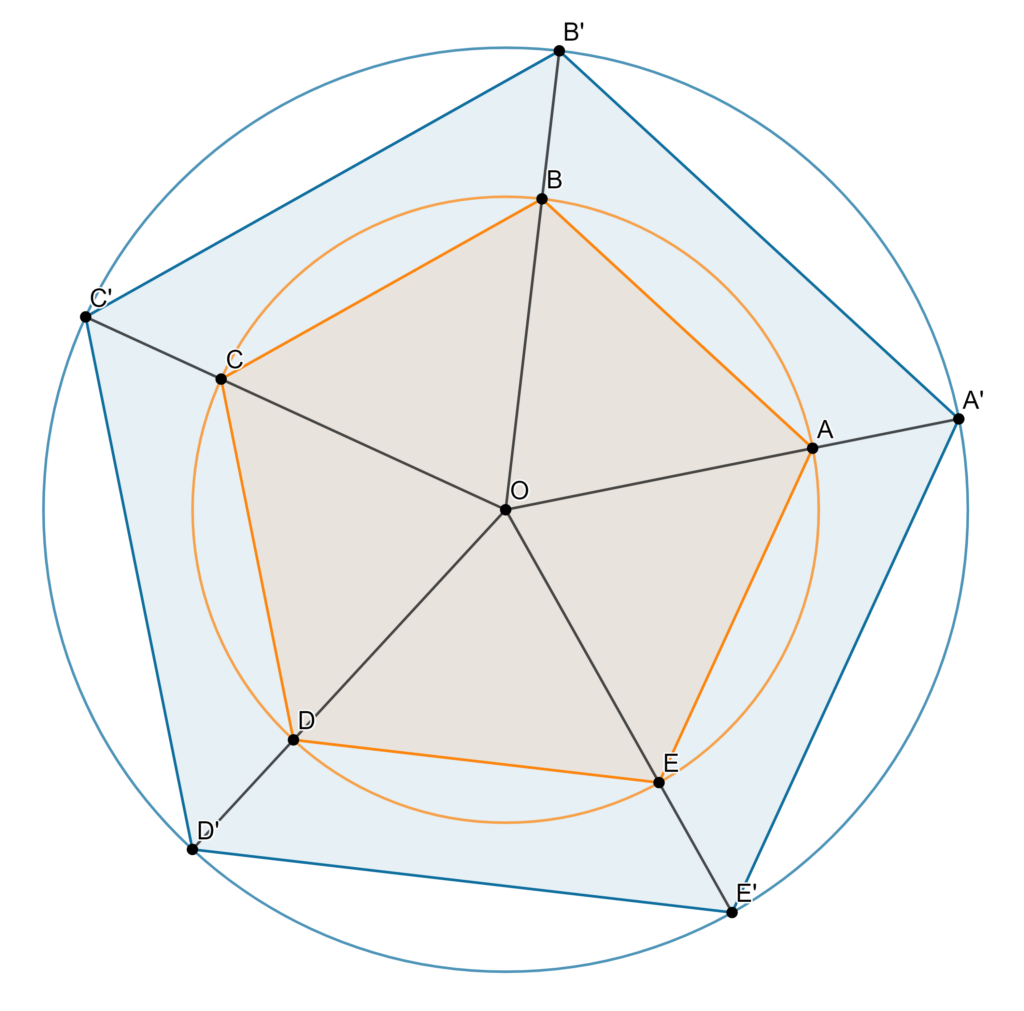
Si on note le rapport des rayons alors on a ainsi les triangles et sont semblables puis en utilisant le théorème de Thalès il vient . Ce raisonnement étant valide pour chaque côté d’un pentagone on peut conclure que le périmètre de est égal à fois celui de . De plus, on peut encore utiliser ce raisonnement quelque soit le nombre de côtés du polygone régulier, ainsi en notant le périmètre du polygone et le périmètre du polygone on obtient pour tout entier naturel la relation . Par linéarité de la limite, il vient ce qui prouve que la circonférence du cercle de rayon et la circonférence du cercle de rayon sont liées par la relation . Cette dernière égalité nous donne finalement puis ce qui achève notre démonstration. Le nombre est à présent bien défini et des calculs informatiques permettent ensuite de déterminer sa valeur avec une grande précision.