L'aire d'un disque - L'univers des mathématiques

L’aire d’un disque de rayon $R$ est donnée par la formule $\pi R^2$ présentée au collège. Comment peut-on démontrer simplement cette formule ? L’astuce est de partager l’aire du disque en un nombre pair de parties égales noté $2n$ puis d’approcher chaque partie du disque par le triangle isocèle qui est inscrit à l’intérieur. On se retrouve donc avec $n$ paires de triangles isocèles. Chacun de ces triangles isocèles possède deux côtés égaux à $R$ puis on note $c_n$ la longueur du dernier côté et $h_n$ la hauteur relative à $c_n$ . Voici par exemple la figure obtenue pour $n=4$ avec 4 paires de triangles isocèles dans le disque :

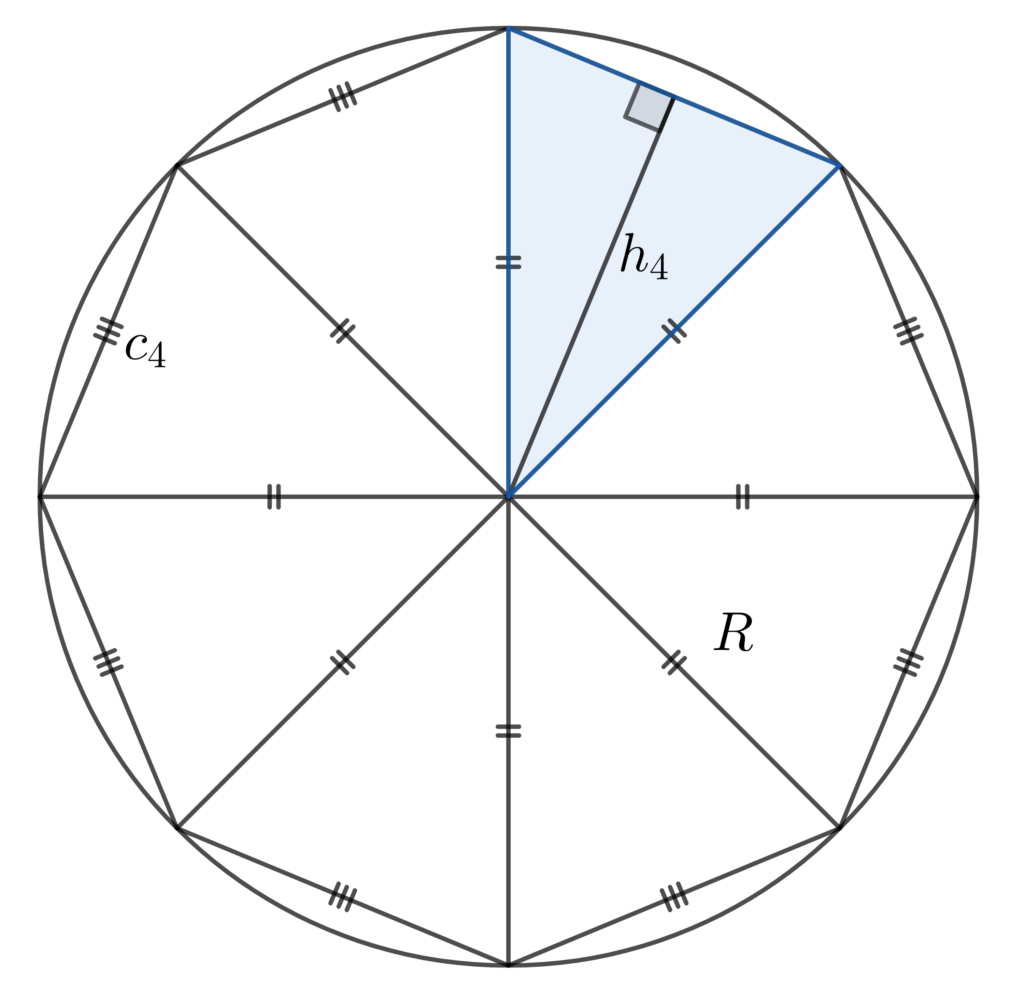
L’aire du disque $\mathscr{A}$ est la limite lorsque $n$ tend vers l’infini de l’aire contenue dans les $2n$ triangles isocèles. Puisque nous avons un nombre pair de triangles isocèles il est possible de les regrouper pour former un parallélogramme comme dans la figure ci-dessous :

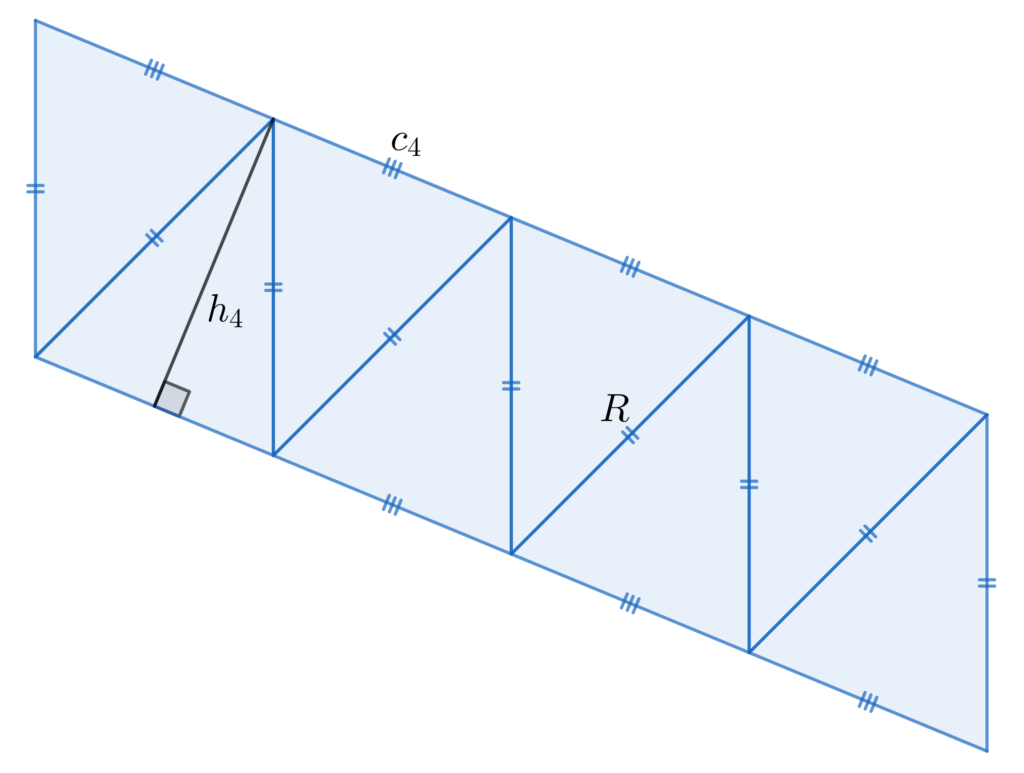
L’aire du parallélogramme représenté dans l’exemple est $4c_4\times h_4$ et ce raisonnement étant valide pour tout nombre entier $n$ on déduit que l’aire formée par tous les triangles isocèles contenus dans le disque est $nc_n\times h_n$ puis on obtient :

$\displaystyle \mathscr{A}=\lim_{n\to+\infty} nc_n\times h_n$

Par définition du nombre Pi on sait que $\lim_{n\to +\infty} 2nc_n=2\pi R$ donc il vient $\lim_{n\to +\infty} nc_n=\pi R$ par linéarité de la limite. De plus d’après le t héorème de Pythagore pour tout nombre entier $n$ on a $h_n=\sqrt{R^2-(c_n/2)^2}$ et comme $\lim_{n\to +\infty} c_n=0$ on déduit que $\lim_{n\to +\infty} h_n=R$ par continuité de la fonction $x\mapsto \sqrt{R^2-(x/2)^2}$ . On peut à présent terminer notre calcul de $\mathscr{A}$ par un produit de limites :

$\displaystyle \mathscr{A}=\lim_{n\to+\infty} nc_n\times h_n=\lim_{n\to+\infty} nc_n\times \lim_{n\to+\infty}h_n=\pi R\times R=\pi R^2$

Partager :

Laisser un commentaire Annuler la réponse