Les pyramides et les cônes

Laisser un commentaire / Articles / Géométrie, Intégration, Limites / Par

Comment peut-on calculer l’aire et le volume d’une pyramide ou d’un cône ? Une pyramide est le solide que l’on obtient en reliant par des segments chacun des points d’un polygone \mathscr{P} à un seul et même point S. On dit que le polygone \mathscr{P} est la base de la pyramide et que le point S est le sommet de la pyramide. Si l’on remplace dans cette définition le polygone \mathscr{P} par un cercle alors on a la définition d’un cône.

Volume d’une pyramide

Rappelons que la hauteur d’une pyramide est la distance entre son sommet et le plan contenant sa base puis commençons par rechercher le volume d’une pyramide. Voici par exemple une pyramide dont la base est un quadrilatère que l’on a représenté en perspective :

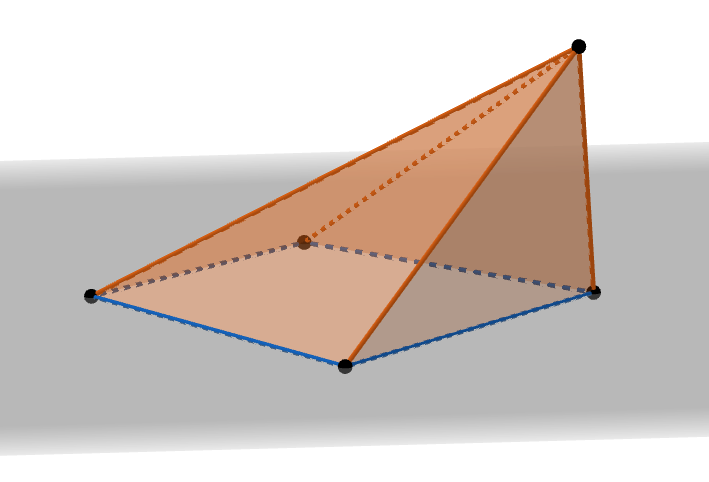
Pour approcher le volume \mathscr{V} de notre pyramide nous allons la diviser en n morceaux puis approcher chacun de ces morceaux par un prisme droit. Les différentes sections de la pyramide se font toutes parallèlement à la base donc perpendiculairement à la hauteur et elles sont régulièrement espacées. Par exemple dans le cas où n=7 les différentes sections vont nous permettre de définir 7 prismes droits que l’on numérote à partir du sommet. Ce cas particulier est représenté dans une vue de profil ci-dessous avec les volumes des différents prismes droits notés v_1,v_2,\dots,v_7 qui permettent d’approcher le volume de la pyramide :

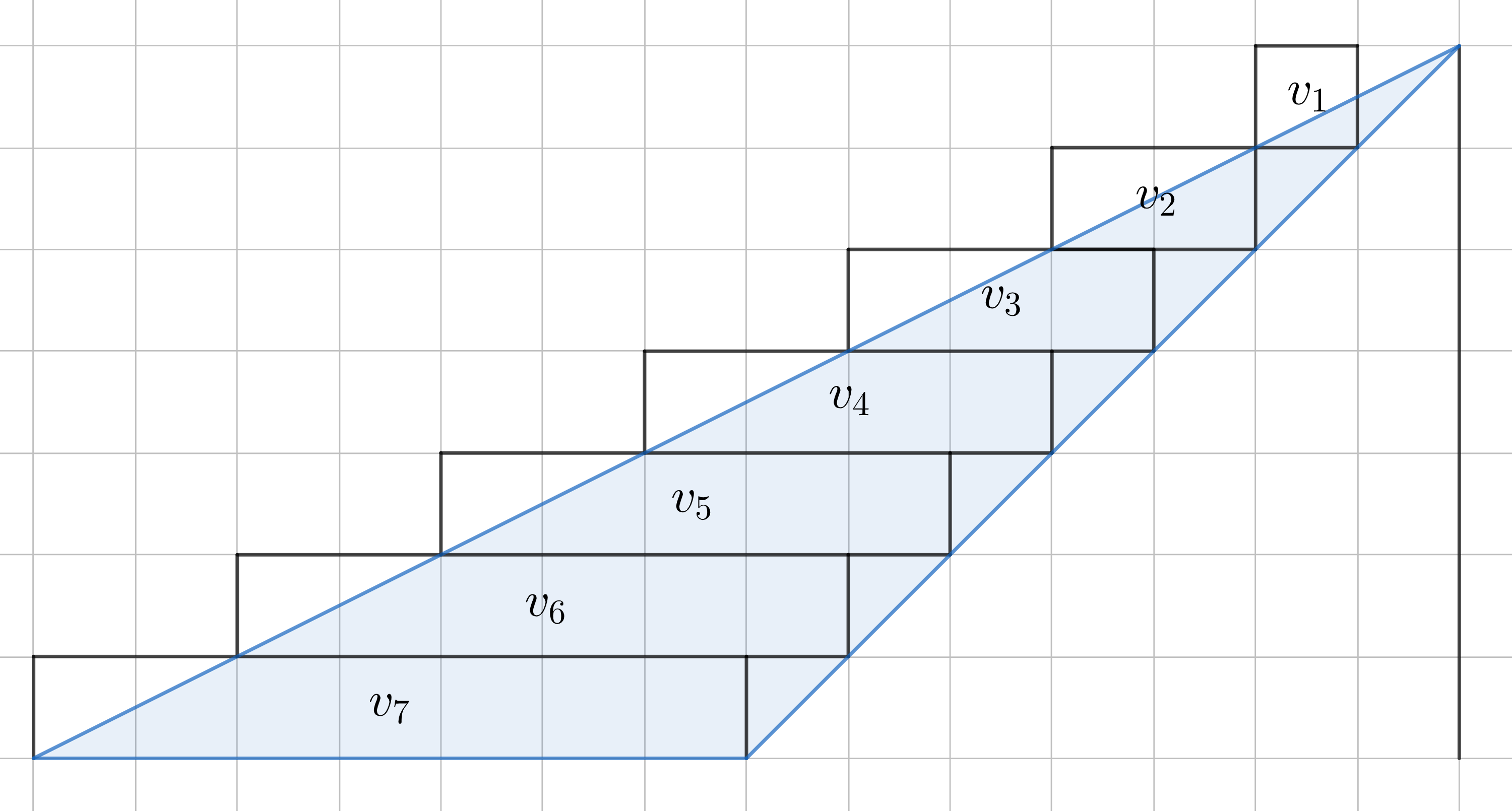
Si on note H la hauteur de la pyramide alors la hauteur de chaque prisme droit est H/n. L’aire de la base B est égale à l’aire de la base du dernier prisme droit de volume v_n. D’après le théorème de Thalès le prisme droit de volume v_k est une réduction du prisme droit de volume v_n et le rapport de cette réduction est \gamma_k=k/n donc l’aire de base du prisme droit de volume v_k est B\gamma_k^2. Le volume de la pyramide est approché par la somme de tous les volumes de prismes droits mais ce calcul sera d’autant plus précis que le nombre n de prismes droits sera élevé ainsi nous obtenons :

\displaystyle \mathscr{V}=\lim_{n\to +\infty} \sum_{k=1}^n v_k = \lim_{n\to +\infty} \sum_{k=1}^n B\gamma_k^2 \times \frac{H}{n}=BH\lim_{n\to +\infty} \frac{1}{n}\sum_{k=1}^n\left(\frac{k}{n}\right)^2

Le calcul de cette dernière limite peut se faire rapidement en utilisant le corollaire de la méthode des rectangles ce qui nous permet d’obtenir l’élégante formule ci-dessous pour le volume d’une pyramide :

\displaystyle \mathscr{V}=BH\int_0^1 x^2 dx = BH\left[ \frac{x^3}{3} \right]_0^1=\frac{1}{3}BH

La base de la pyramide représentée en perspective dans l’exemple est un quadrilatère mais les raisonnements utilisés restent valides quelque soit le nombre de côtés N que possède la base. On peut ainsi conclure que la formule est vraie pour n’importe quelle pyramide.

Volume d’un cône

Considérons maintenant un cône dont la base est un cercle \mathscr{C} et notons S le sommet du cône. On va approcher ce cône par des pyramides possédant le même sommet S dont la base est un polygone régulier à N côtés inscrit dans le cercle \mathscr{C}. La hauteur de chacune de ces pyramides est toujours H mais l’aire de base B_N varie suivant le nombre de côtés N. On sait que l’aire d’un polygone régulier à N côtés se rapproche de l’aire de son cercle inscrit à mesure que N augmente donc on a \lim_{N\to +\infty} B_N = B avec B l’aire de base du cône. En utilisant la formule du volume d’une pyramide et la linéarité de la limite on peut donc affirmer que le volume du cône est :

\displaystyle \mathscr{V}=\lim_{N\to +\infty} \frac{1}{3}B_NH = \frac{1}{3}BH

Aire d’une pyramide régulière

Une pyramide est dite régulière lorsque sa base est un polygone régulier et que sa hauteur passe par le centre du polygone de base. On se propose à présent de rechercher l’aire d’une pyramide régulière dont la base possède N côtés. On peut noter c_N la longueur commune de tous les côtés de la base puis R_N la distance commune qui sépare chaque côté du polygone régulier à son centre. Voici par exemple une illustration pour N=5 :

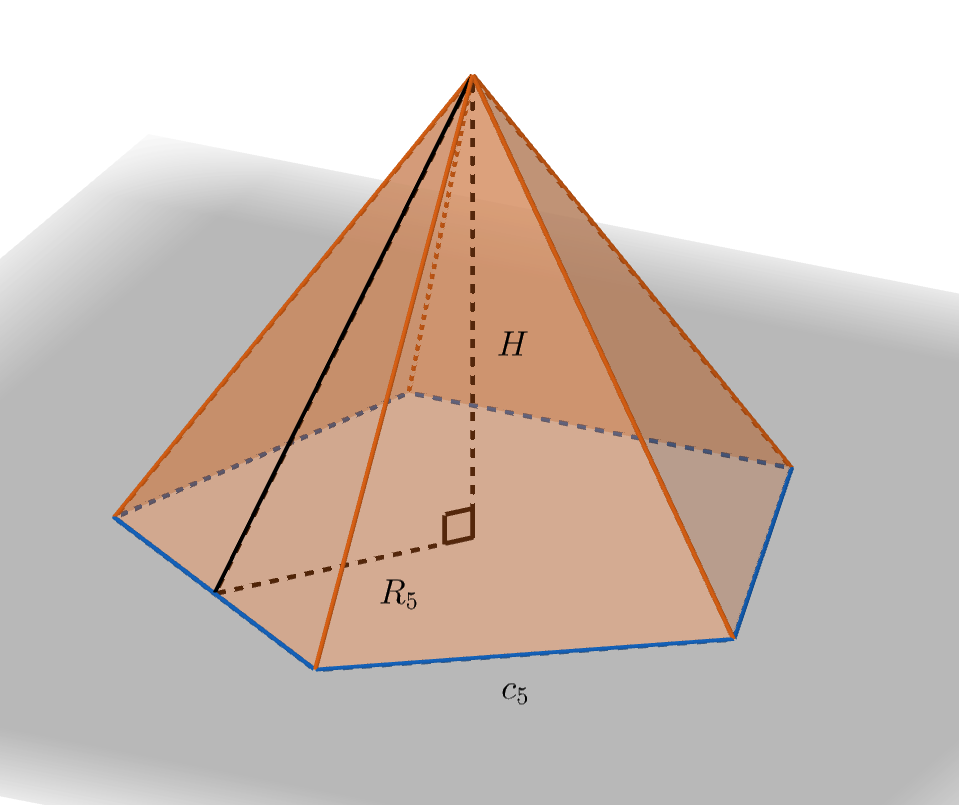
D’après le théorème de Pythagore nous obtenons la formule ci-dessous pour l’aire \mathscr{A} d’une pyramide régulière dont la base possède N côtés :

\displaystyle \mathscr{A}=B+N\times \frac{c_N}{2}\sqrt{R_N^2+H^2}

Aire d’un cône de révolution

Un cône est dit de révolution lorsque sa hauteur passe par le centre du cercle de base. On étudie maintenant un cône de révolution en notant S son sommet et \mathscr{C} son cercle de base puis R le rayon de \mathscr{C}. On approche ce cône par des pyramides régulières possédant le même sommet S dont la base est un polygone régulier à N côtés inscrit dans le cercle \mathscr{C}. L’étude du nombre Pi nous a permis d’obtenir la limite \lim_{N\to +\infty} Nc_N=2\pi R ainsi que la limite \lim_{N\to +\infty} R_N=R. En utilisant la formule de l’aire d’une pyramide régulière et la continuité de la fonction x\mapsto \sqrt{x^2+H^2} on peut donc affirmer que l’aire du cône de révolution est :

\displaystyle \mathscr{A}=B+\lim_{N\to +\infty} N\times \frac{c_N}{2}\sqrt{R_N^2+H^2}=B+ \frac{2\pi R}{2}\sqrt{R^2+H^2}=B+\pi R\sqrt{R^2+H^2}

Aire latérale d’un tronc de cône de révolution

Pour terminer cet article, on va rechercher l’aire latérale d’un tronc de cône de révolution ce qui nous sera utile pour étudier l’aire d’une sphère. Un tronc de cône est le solide que l’on obtient lorsque l’on découpe un cône parallèlement à sa base. On note R le rayon du cône initial et H sa hauteur. La section de ce cône permet d’obtenir un cône réduit dont le rayon est noté r et la hauteur h. La longueur qui relie le sommet du cône initial à son cercle de base se retrouve en partie dans le tronc du cône, cette partie est appelée la génératrice du tronc de cône et elle est notée g comme dans la représentation en perspective ci-dessous :

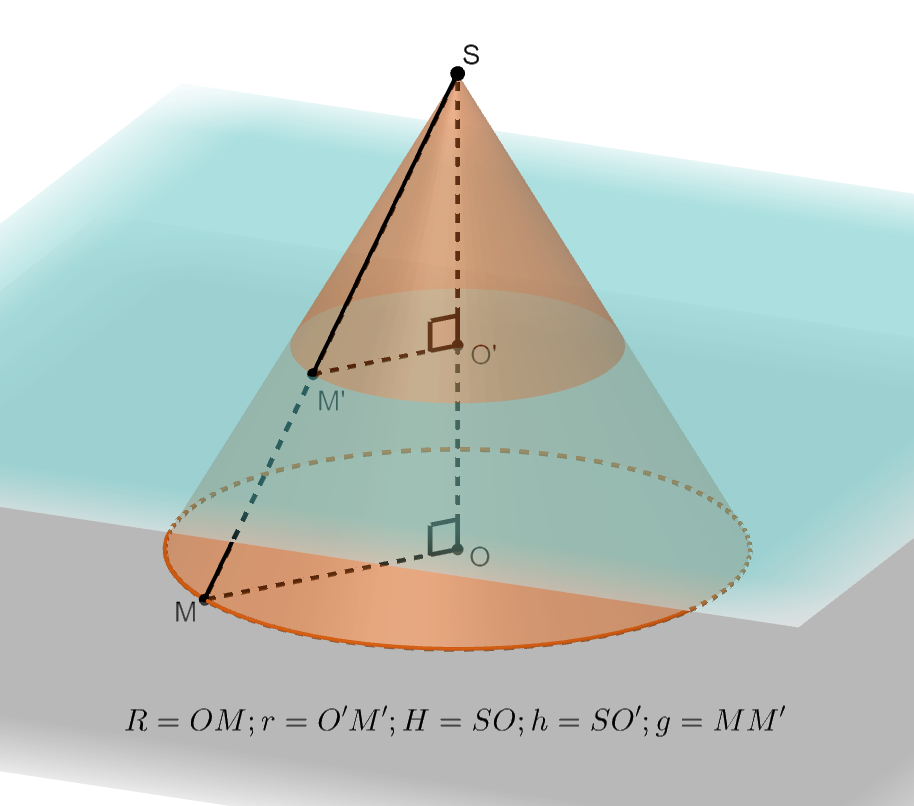
Le coefficient de réduction entre les deux cônes est \gamma = r/R= h/H et si on note \rho=(R+r)/2 la moyenne des deux rayons alors on obtient une belle formule pour le calcul de l’aire latérale \mathscr{A}' du tronc de cône :

\displaystyle \mathscr{A'}=\pi R\sqrt{R^2+H^2}-\pi r\sqrt{r^2+h^2}=\pi R\sqrt{R^2+H^2}-\gamma^2\pi R\sqrt{R^2+H^2}=\pi R\sqrt{R^2+H^2}(1-\gamma^2)= \pi R\sqrt{R^2+H^2} (1-\gamma)(1+\gamma)=\pi(R+r)\sqrt{R^2+H^2}(1-\gamma)=\pi(R+r)\sqrt{(R^2+H^2)(1-\gamma)^2}=\pi(R+r)\sqrt{R^2(1-\gamma)^2+H^2(1-\gamma)^2}=\pi(R+r)\sqrt{(R-r)^2+(H-h)^2}=2\pi\rho g

Laisser un commentaire

Votre adresse e-mail ne sera pas publiée. Les champs obligatoires sont indiqués avec *