L’aire et le volume d’une sphère

Laisser un commentaire / Articles / Géométrie, Intégration, Limites / Par

Comment peut-on calculer l’aire et le volume d’une sphère ? Cet article propose des démonstrations mathématiques des formules classiques que l’on présente au collège. On considère une sphère de rayon R mais pour simplifier la présentation on décide d’étudier plutôt la demi-sphère associée.

Volume d’une sphère

Pour approcher le volume d’une demi-sphère \mathscr{V}' nous allons la diviser en n morceaux puis approcher chacun de ces morceaux par un cylindre. Les différentes sections de la demi-sphère se font toutes parallèlement à la base et elles sont régulièrement espacées. Par exemple dans le cas où n=5 les différentes sections vont nous permettre de définir 5 cylindres que l’on numérote à partir de la base. Ce cas particulier est représenté dans une vue de profil ci-dessous avec les volumes des différents cylindres notés v_0, v_1,\dots ,v_4 qui permettent d’approcher le volume de la demi-sphère :

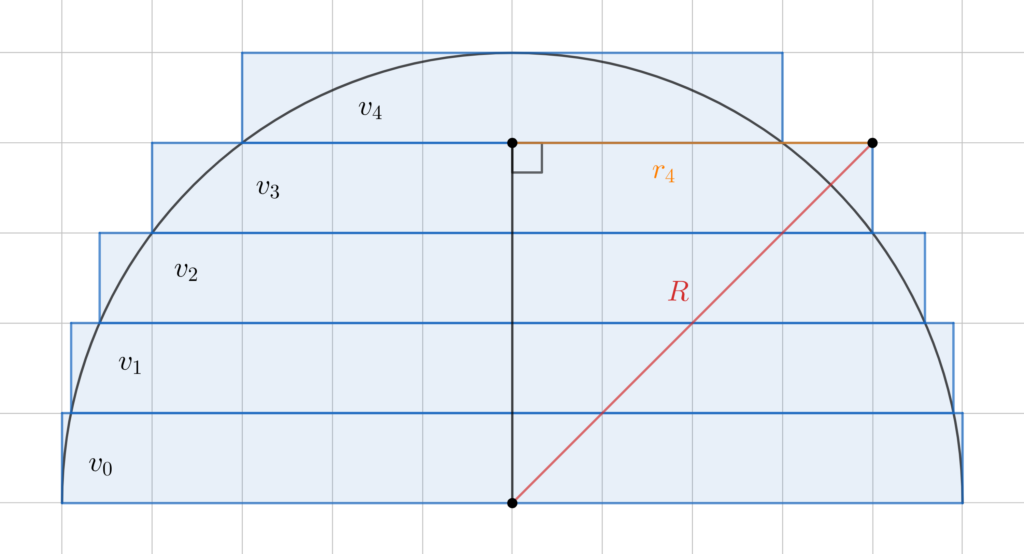
Si on note R le rayon de la demi-sphère alors la hauteur de chaque cylindre est R/n. L’aire de la base du cylindre de volume v_k est une aire de disque qui est égale à \pi(R^2-(kR/n)^2) d’après le théorème de Pythagore. Le volume de la demi-sphère est approché par la somme de tous les volumes de cylindres mais ce calcul sera d’autant plus précis que le nombre n sera élevé ainsi nous obtenons :

\displaystyle \mathscr{V}'=\lim_{n\to+\infty} \sum_{k=0}^{n-1} v_k = \lim_{n\to+\infty} \sum_{k=0}^{n-1} \pi R^2\left(1-\left(\frac{k}{n}\right)^2\right)\times \frac{R}{n}=\pi R^3\lim_{n\to+\infty} \frac{1}{n}\sum_{k=0}^{n-1}\left(1-\left(\frac{k}{n}\right)^2\right)

Le calcul de cette dernière limite peut se faire rapidement en utilisant le corollaire de la méthode des rectangles ce qui nous permet d’obtenir l’élégante formule ci-dessous pour le volume d’une sphère :

\displaystyle \mathscr{V}=2\mathscr{V}'=2\pi R^3 \int_0^1 1-x^2dx=2\pi R^3\left[ x-\frac{x^3}{3}\right]_0^1=2\pi R^3\left(1-\frac{1}{3}\right)=\frac{4}{3}\pi R^3

Aire d’une sphère

Nous allons maintenant nous intéresser à l’aire \mathscr{A}' d’une demi-sphère. Il est possible d’approcher une courbe par des segments élémentaires à condition que ces segments possèdent leurs extrémités sur la courbe. De même il est possible d’approcher une aire \mathscr{A}' par des surfaces élémentaires à condition que ces surfaces possèdent leurs bords sur \mathscr{A}'. C’est pour cette raison qu’il ne faut pas utiliser des cylindres pour approcher l’aire de la demi-sphère mais plutôt des troncs de cônes. La demi-sphère est à nouveau divisée en n morceaux mais chacun de ces morceaux est approché cette fois par l’aire latérale d’un tronc de cône. Les différentes sections de la demi-sphère sont toujours parallèles à la base et régulièrement espacées. Dans le cas où n=5 ces sections vont nous permettre de définir 5 troncs de cônes que l’on numérote à partir de la base. Ce cas particulier est représenté dans une vue de profil ci-dessous avec les aires latérales des différents troncs de cônes notées a_1, a_2,\dots ,a_5 qui permettent d’approcher l’aire de la demi-sphère :

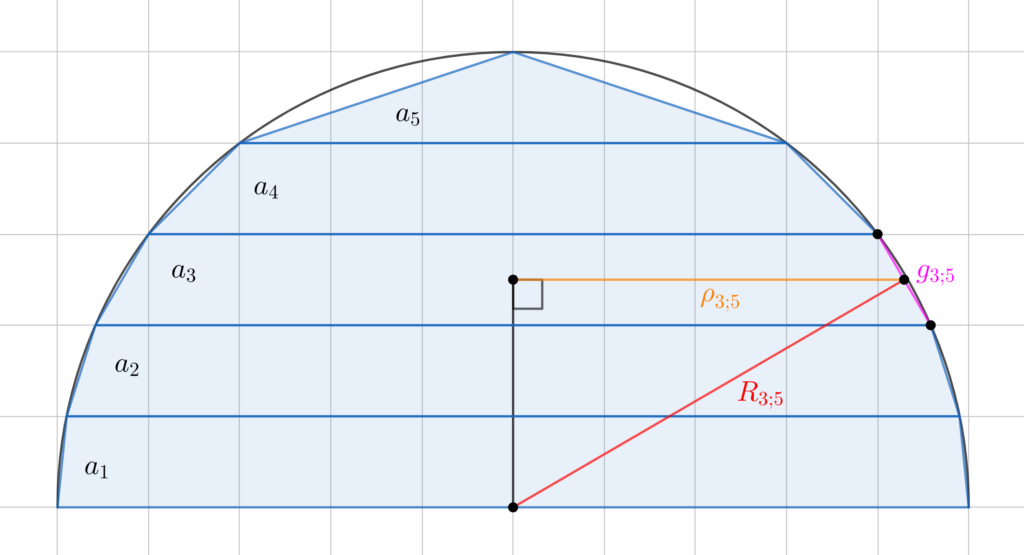
Cette fois-ci on opte pour une notation plus précise des paramètres du tronc de cône d’aire latérale a_k : son rayon moyen est noté \rho_{kn} et sa génératrice est notée g_{kn}. La distance entre le milieu de la génératrice g_{kn} et le centre de la demi-sphère est notée R_{kn}. On sait d’après l’étude des troncs de cônes que a_k=2\pi\rho_{kn}g_{kn} et pour calculer \mathscr{A}' il nous faut sommer les aires a_1, a_2,\dots ,a_n avec n le plus grand possible donc on a :

\displaystyle \mathscr{A}'=\lim_{n\to+\infty} \sum_{k=1}^n a_k= 2\pi\lim_{n\to+\infty} \sum_{k=1}^n \rho_{kn}g_{kn}

Pour pouvoir avancer dans notre calcul, il nous faut regarder plus en détail la génératrice g_{kn} d’un tronc de cône d’aire latérale a_k. C’est ce que l’on se propose de faire dans l’illustration ci-dessous :

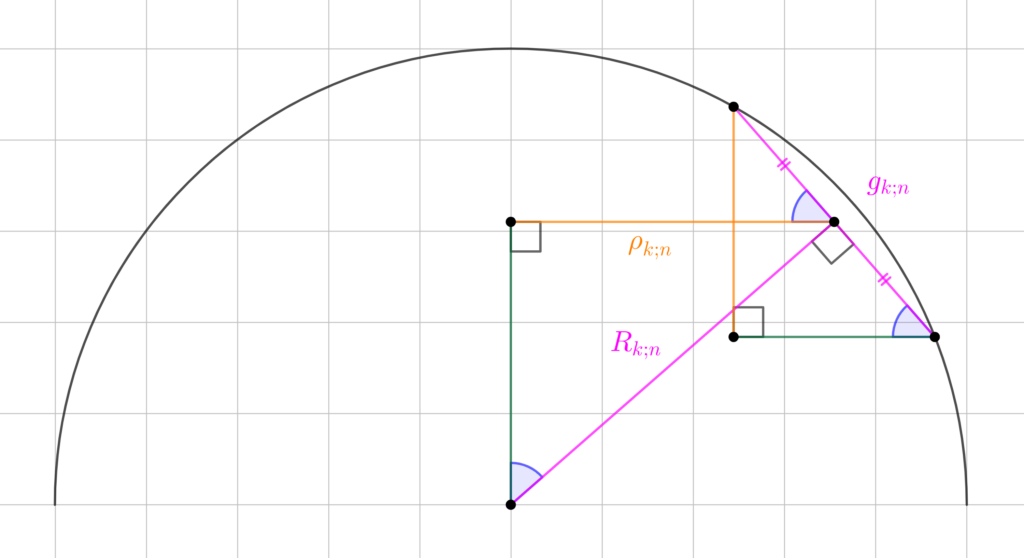
Rappelons que chaque tronc de cône a une hauteur égale à R/n. La figure précédente nous permet de remarquer deux triangles semblables donc d’après le théorème de Thalès on a \rho_{kn}/ (R/n) = R_{kn} / g_{kn} puis il vient :

\displaystyle \mathscr{A}'=2\pi\lim_{n\to+\infty} \sum_{k=1}^n \rho_{kn}g_{kn}=2\pi\lim_{n\to+\infty} \sum_{k=1}^n \left(\frac{R}{n}\right)\frac{R_{kn}}{g_{kn}}g_{kn}=2\pi R\lim_{n\to+\infty} \frac{1}{n}\sum_{k=1}^n R_{kn}

Il reste à traiter le calcul de limite, on remarque que pour tout entier k on a R_{1n}\leq R_{kn}\leq R. De plus on a \rho_{1n}\leq R_{1n} avec \rho_{1n} qui est la moyenne de R et \sqrt{R^2-(R/n)^2} ce qui nous donne les inégalités suivantes pour tout entier k compris entre 1 et n :

\displaystyle \frac{R+\sqrt{R^2-\left(\frac{R}{n}\right)^2}}{2}\leq R_{kn}\leq R

On somme ensuite ces n inégalités puis l’on divise tout par n afin d’obtenir l’encadrement suivant :

\displaystyle \frac{R+\sqrt{R^2-\left(\frac{R}{n}\right)^2}}{2}\leq \frac{1}{n}\sum_{k=1}^n R_{kn}\leq R

Par passage à la limite dans ce dernier encadrement on déduit que \lim_{n\to+\infty} \frac{1}{n}\sum_{k=1}^n R_{kn}=R et ainsi que \mathscr{A}'=2\pi R^2. Nous pouvons à présent conclure que l’aire d’une sphère est :

\mathscr{A}=2\mathscr{A}'=4\pi R^2

Laisser un commentaire

Votre adresse e-mail ne sera pas publiée. Les champs obligatoires sont indiqués avec *