Une question d'âge - L'univers des mathématiques

Alex dit à Béa : « J’ai deux fois l’âge que vous aviez quand j’avais l’âge que vous avez. Quand vous aurez l’âge que j’ai actuellement nous aurons à nous deux 63 ans. » Quels sont les âges de Alex et Béa ?

Indice

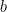On peut désigner par les lettres $a$ et $b$ les âges respectifs de Adrien et Béa. L’affirmation fait référence à trois moments différents que l’on peut numéroter : 1 pour le passé, 2 pour le présent et 3 pour le futur. On se retrouve ainsi avec 6 âges inconnus à rechercher : les âges $(a_1,a_2,a_3)$ de Adrien et les âges $(b_1,b_2,b_3)$ de Béa aux différents moments considérés.

Solution

L’affirmation « J’ai deux fois l’âge que vous aviez quand j’avais l’âge que vous avez. » se traduit par les deux équations $a_2=2b_1$ et $a_1=b_2$ . L’affirmation « Quand vous aurez l’âge que j’ai actuellement nous aurons à nous deux 63 ans. » se traduit par les deux équations $b_3=a_2$ et $a_3+b_3=63$ . Le texte nous fournit ainsi 4 équations à 6 inconnues mais pour obtenir une solution unique, comme le suggère la question, il nous faut 2 équations supplémentaires. Pour cela, utilisons le principe selon lequel une différence d’âge entre deux personnes se conserve dans le temps : on obtient alors les 2 équations $a_1-b_1=a_2-b_2=a_3-b_3$ . Passons à présent à la résolution en remarquant que :

$\displaystyle a_1-b_1=a_2-b_2\implies b_2-b_1=2b_1-b_2\implies 3b_1=2b_2\implies 2b_2=3/2a_2=3/2b_3\implies b_2=3/4b_3$