Le théorème de Pythagore affirme que dans un triangle rectangle en
on a l’égalité suivante :
. Cette égalité permet de lier les 3 longueurs d’un triangle rectangle et en particulier de déterminer l’une des longueurs à partir des deux autres. Selon certains récits antiques, la découverte de ce théorème il y a plus de 2500 ans est attribuée au mathématicien grec Pythagore et sa démonstration au mathématicien grec Euclide. Ce dernier a consigné ce théorème dans l’un de ses ouvrages sous la forme suivante :
« Aux triangles rectangles, le carré du côté qui soutient l’angle droit, est égal aux carrés des deux autres côtés. »
Eléments – Euclide
Comment peut-on démontrer ce théorème simplement ? La démonstration la plus simple repose sur des considérations d’aires. On considère un triangle rectangle en
puis on trace des droites perpendiculaires et on reporte les longueurs pour obtenir la figure ci-dessous :
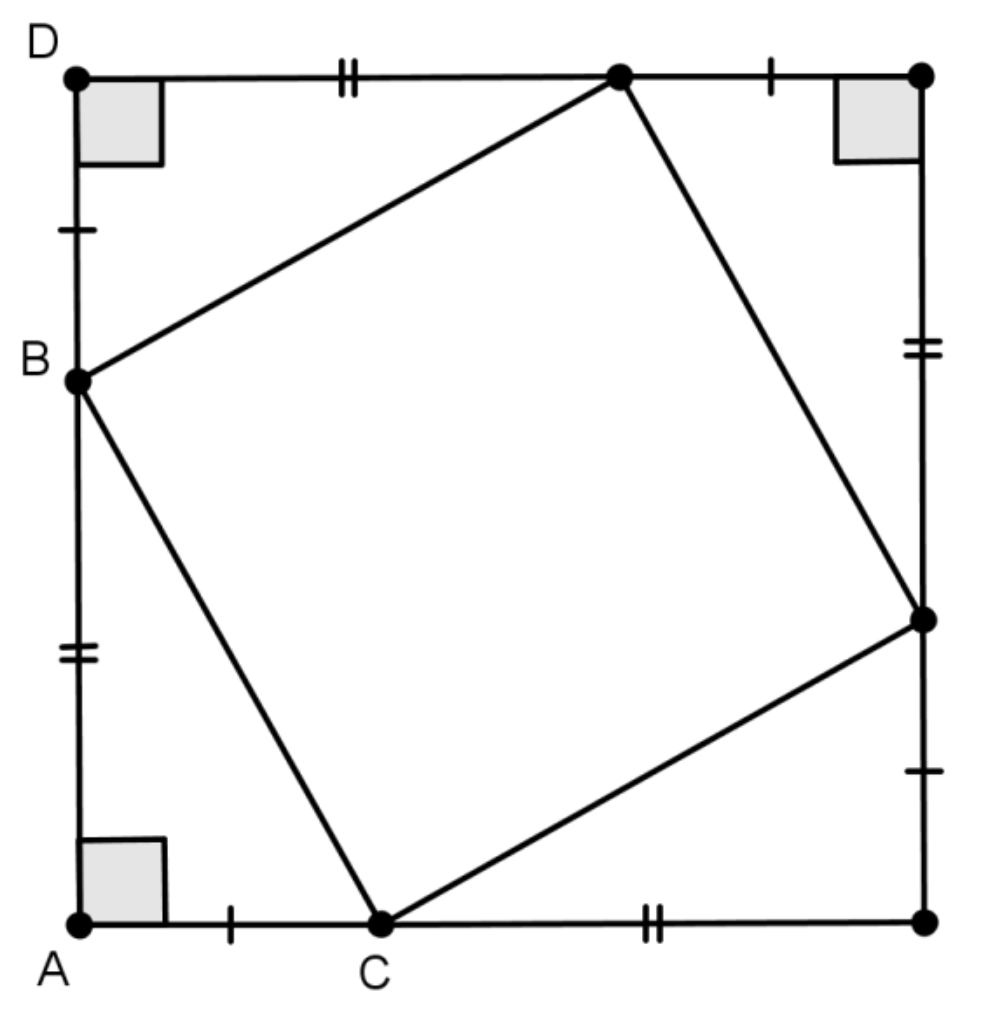
Le quadrilatère de côté est clairement un carré puisque la somme des angles du triangle
vaut
. Calculons à présent l’aire du carré de côté
de deux façons différentes en utilisant uniquement les longueurs du triangle
, on obtient d’une part :
D’autre part, l’aire du triangle étant égale à
l’aire du carré de côté
est aussi :
Les deux façons de calculer l’aire du carré de côté donnent le même résultat ainsi on a
puis en retranchant
aux deux membres de cette dernière égalité on obtient l’égalité de Pythagore :

Ping : La racine cubique de 2 - L'univers des mathématiques