Le nombre d’or

Considérons un segment [AB] puis un point C sur le segment [AB] plus proche de A que de B. Nous obtenons alors en tout 3 segments :

– un segment [AC] de petite longueur.
– un segment [BC] de longueur moyenne.
– un segment [AB] de grande longueur.

Le nombre d’or est la réponse à une question d’ordre esthétique :

Où faut-il placer le point C pour que la proportion entre les 3 différentes longueurs soit conservée ?

Cette proportion conservée (la grande longueur divisée par la longueur moyenne ou la longueur moyenne divisée par la petite longueur) peut être notée et la conservation des proportions s’écrit alors :

Les calculs suivants montrent que est en fait une solution d’une équation du second degré :

Nous pouvons à présent conclure que est la solution positive de cette équation du second degré c’est à dire :

Cette proportion est appelée le nombre d’or. Il faut placer le point C de sorte que .

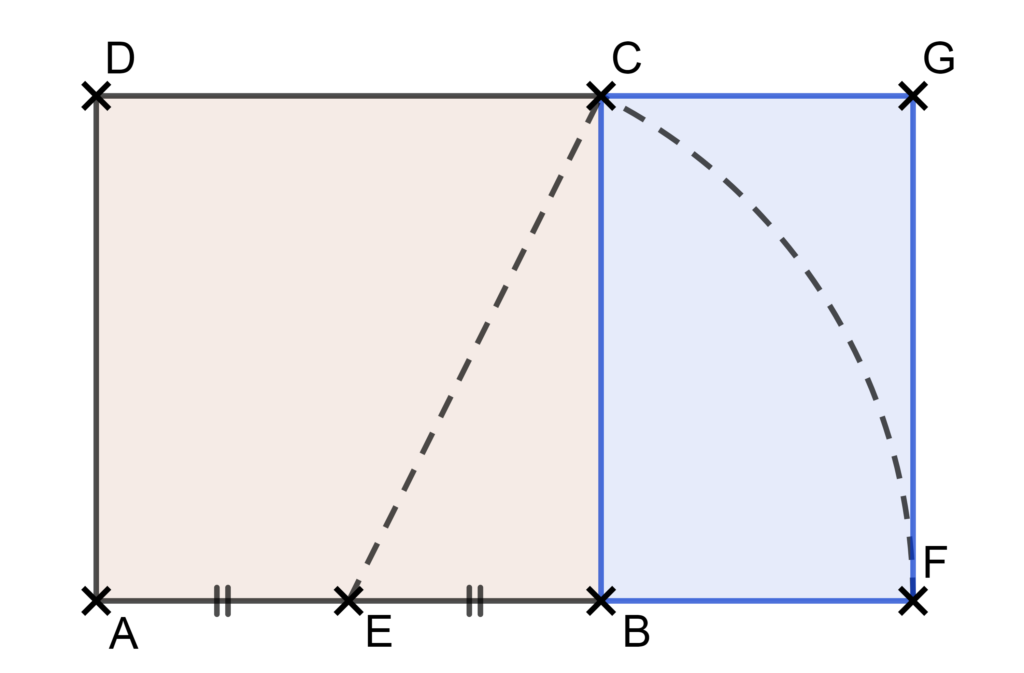
Observez l’image ci-dessous. Pour construire cette figure on est parti d’un carré ABCD et on a placé un point E au milieu de [AB]. Le cercle de centre E passant par C coupe la droite (AB) en F. On place ensuite le point G de sorte que AFGD soit un rectangle. La construction obtenue est remarquablement esthétique car le rectangle AFGD est alors composé d’un carré et d’un rectangle BFGC qui est une réduction de AFGD. Ces deux rectangles sont appelés des rectangles d’or car pour chacun d’eux le rapport entre la longueur et la largeur est !