Le théorème de Pythagore nous permet d’obtenir facilement une construction géométrique de la racine carrée de 2 (il suffit de considérer la diagonale d’un carré de côté 1). Qu’en est-il de la racine cubique de 2 ? Ce nombre est la solution du superbe problème ci-dessous :
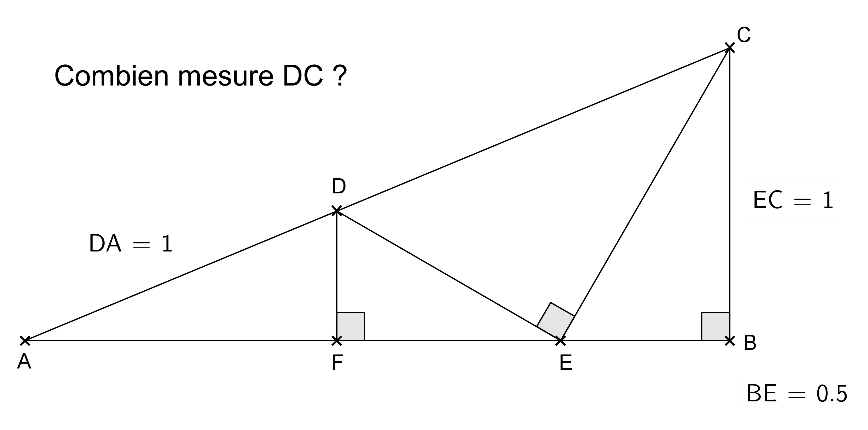
En fait, la racine cubique de 2 est un nombre non constructible à la règle et au compas d’après les travaux du mathématicien français Wantzel. La figure précédente est ainsi impossible à réaliser précisément à l’aide des instruments classiques de géométrie.
« Tout nombre constructible x est racine d’un polynôme à coefficients entiers et le degré du polynôme minimal admettant x comme zéro est une puissance de 2.«
Théorème de Wantzel
Dans le cas présent, le polynôme minimal de la racine cubique de 2 sur le corps des réels est 
