Le bon nombre de triangles

Cette figure est un pentagone contenant une étoile. On peut commencer par compter les triangles qui n’ont aucun côté sur le pentagone (leurs côtés sont alors sur l’étoile) puis les triangles qui possèdent un seul côté sur le pentagone et enfin les triangles qui possèdent deux côtés sur le pentagone.

Pour faciliter le comptage, donnons des noms aux points de la figure :

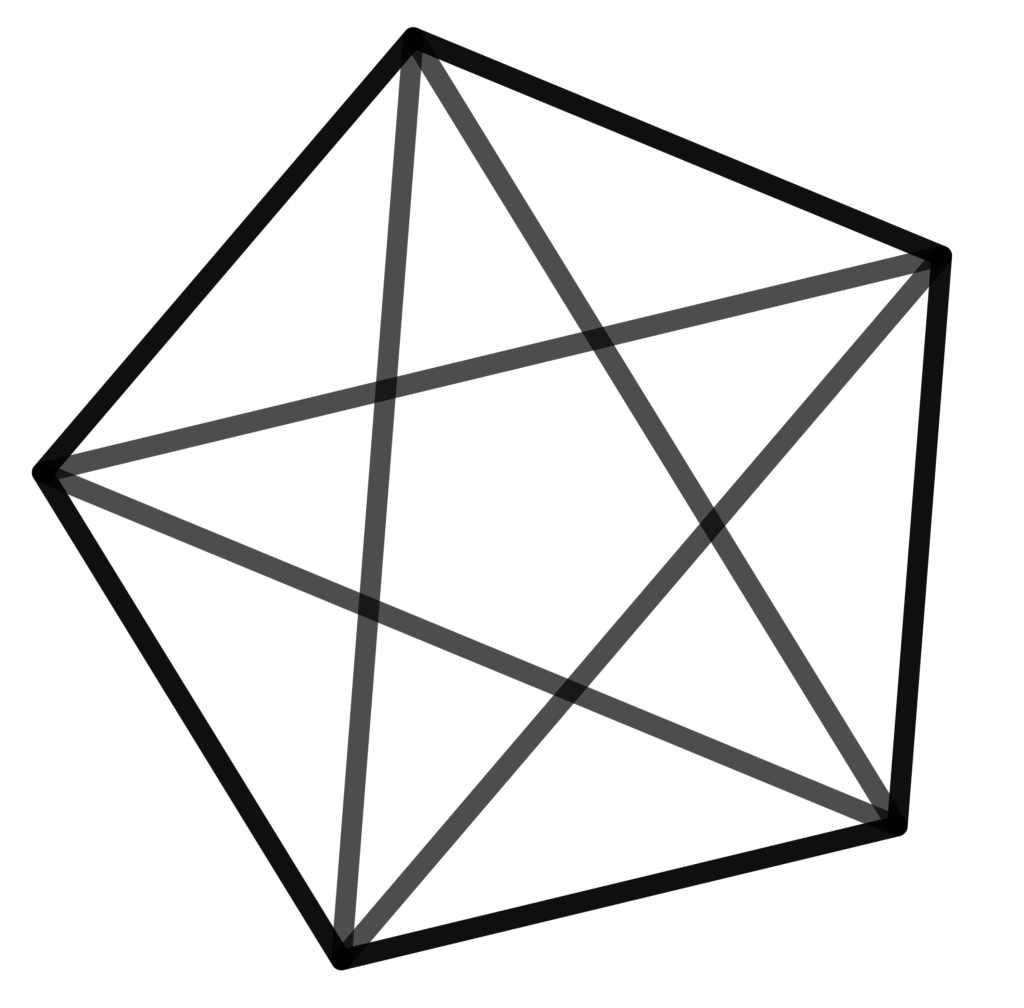
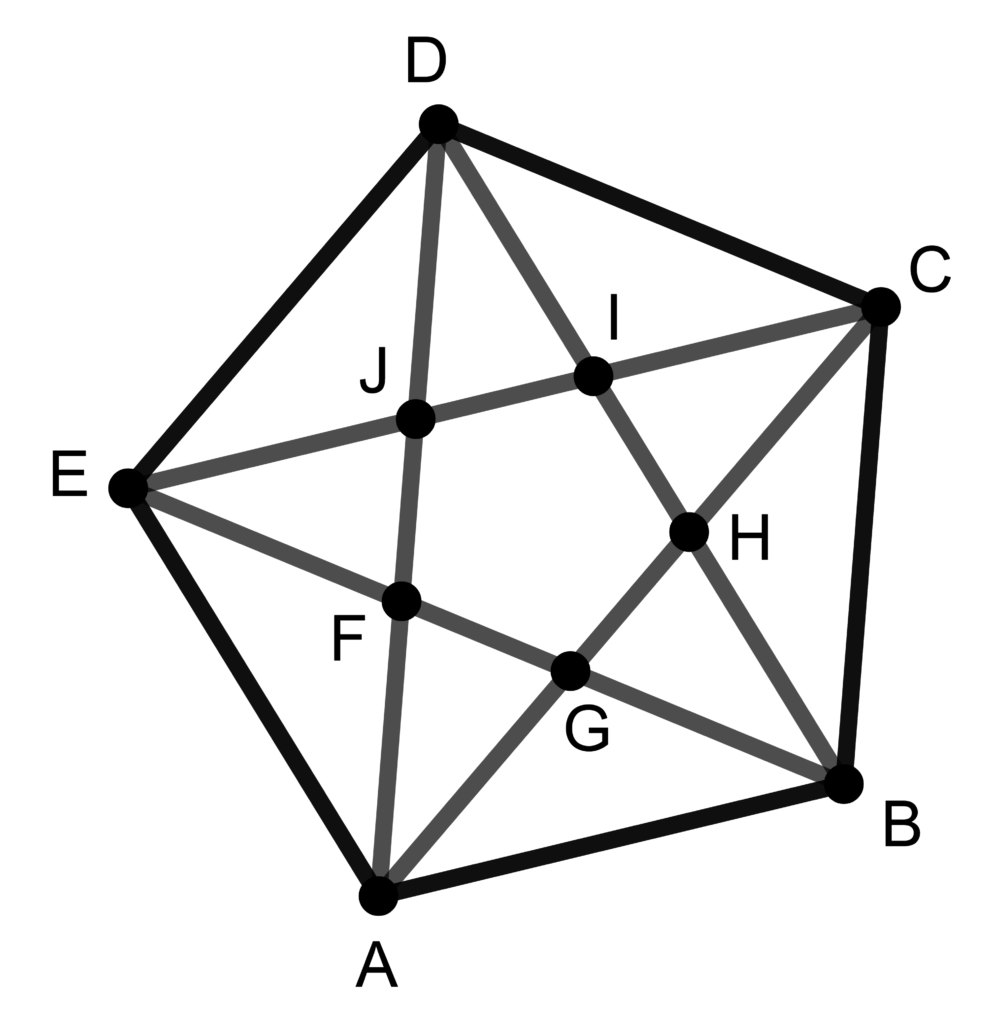
Les triangles qui n’ont aucun côté sur le pentagone sont les triangles sur l’étoile, ils peuvent être formés par l’un des 5 grands segments de l’étoile (ACJ – DBF – ECG – ADH – EBI) ou par des segments plus petits (FGA – GHB – HIC – IJD – JFE). Il y a donc 10 triangles qui n’ont aucun côté sur le pentagone.

Comptons à présent les triangles qui possèdent un seul côté sur le pentagone. Si ce côté sur le pentagone est [AB] alors il y a 4 possibilités (ABF – ABG – ABH – ABD) mais comme il y a 5 choix possibles pour le côté sur le pentagone on peut conclure qu’il y a triangles qui possèdent un seul côté sur le pentagone.

Il reste à compter les triangles qui possèdent deux côtés sur le pentagone et il y a 5 possibilités pour cela (ABC – BCD – CDE – DEA – EAB).

Finalement, au total il y a triangles dans cette figure.