Considérons un certain nombre de points dans un repère : comment déterminer une droite qui approche au mieux ces points ? Pour aborder correctement ce problème, il faut déjà définir ce que signifie l’expression « approcher au mieux » et pour cela il faut décider d’une règle permettant de mesurer les écarts entre les points et la droite. On va convenir de mesurer ces écarts parallèlement à l’axe des ordonnées comme dans l’illustration dynamique ci-dessous :
Dans cette illustration, on considère cinq points dans un repère orthonormé et on souhaite approcher ces points avec une droite
. Les écarts entre les points et la droite sont représentés en rouge. L’erreur d’approximation de la droite
pour approcher les points
est la somme de ces écarts
. L’avantage de décider de mesurer les écarts de cette façon est que cela permet d’approcher ensuite l’ensemble de points par une fonction affine.
Ce problème a déjà été étudié et résolu lorsque l’on décide de considérer plutôt les carrés des écarts : c’est la méthode des moindres carrés indépendamment élaborée par Legendre et Gauss au début du 19-ème siècle. L’objectif de cet article est toutefois différent, il s’agit d’examiner ce qui se passe lorsque l’on décide de ne pas mettre au carré les écarts.
La question à présent est claire : comment choisir les points et
pour que la droite
puisse approcher les points
avec une erreur
minimale ? Dans l’illustration dynamique précédente, vous pouvez déplacer les points
et
afin de rechercher une position optimale.
Peut être avez-vous trouvé cette réponse surprenante à force d’essayer : il faut aligner les points et
avec les points
et
. La droite optimale pour approcher les points
est en fait la droite
! Le théorème présenté dans cet article affirme en effet qu’il existe toujours deux points dans l’ensemble de points à approcher qu’il faut simplement relier pour obtenir la droite optimale recherchée. Il existe ainsi un couple de points qui peut servir de modèle pour approcher l’ensemble des points considéré au départ. Ce théorème fonctionne dans un repère quelconque et pour un nombre de points aussi grand que l’on souhaite. Il fournit de plus une méthode rapide et pratique pour trouver les deux points en question à relier :
Choisir un point de référence au hasard.
Calculer le total
des écarts absolus d’abscisses entre le point de référence et les autres points.
Considérer une droite parallèle à l’axe des ordonnées qui passe par le point de référence et qui tourne dans le sens direct (antihoraire) : à mesure que cette droite tourne elle passe par des points, ajouter au fur et à mesure les écarts absolus d’abscisses jusqu’à trouver le premier point pour lequel la somme dépasse
.
Prendre pour référence le point trouvé dans l’étape précédente et recommencer.
Au bout d’un certain nombre d’étapes les points trouvés sont tous alignés sur la droite recherchée.
Appliquons ce théorème dans l’exemple proposé en introduction :
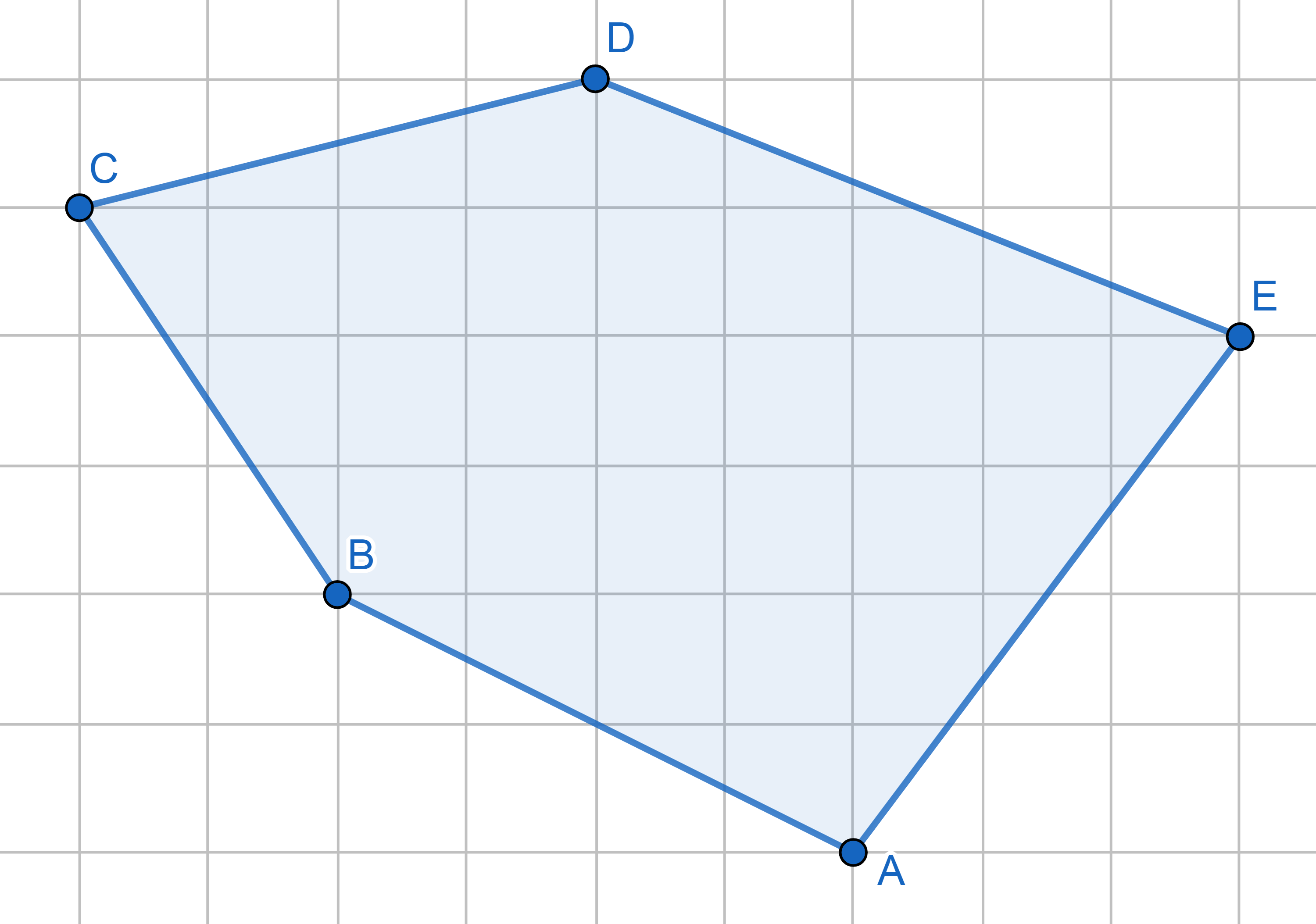
On va choisir au hasard comme point de référence pour débuter les calculs. On considère une droite verticale qui passe par
et qui tourne dans le sens direct : cette droite passe dans l’ordre par les points
. Les écarts absolus d’abscisses correspondants sont
et le total est
. La moitié de ce total est obtenue au point
car
et
. On prend à présent
comme point de référence, en tournant dans le sens direct à partir de
on obtient dans l’ordre
ce qui nous donne les écarts
puis la moitié du total de
est obtenue au point
. On prend maintenant
comme point de référence, en tournant dans le sens direct on obtient les points
et les écarts
puis la moitié du total de
est obtenue au point
. Le théorème conduit à présent sur une boucle infinie entre les points
et
ce qui signifie que la droite optimale est
.
On peut résumer les calculs précédents en disant que le théorème a généré la suite de quatre points : . Il est possible de tester le théorème avec un grand nombre de points en utilisant le code Python suivant :
def horizon(points,indice):
pts = [[(points[i][1] - points[indice-1][1])/(points[i][0] - points[indice-1][0]),points[i][0],points[i][0] - points[indice-1][0],i+1] for i in range(len(points)) if i != indice-1]
total = 0
for pt in pts:
total += abs(pt[2])
pts.sort()
somme = 0
for i in range(len(pts)):
somme += abs(pts[i][2])
if somme >= total/2:
reponse = pts[i][3]
break
return reponse
def coupleSym(points, indice=1):
indices = []
while indice not in indices:
indices.append(indice)
indice = horizon(points,indice)
indices.append(indice)
return indicesCe code a été utilisé pour déterminer le couple de points qui définit la droite optimale avec un ensemble de points. Le théorème a généré une suite comportant seulement six points puis le couple optimal a été relié par un segment rouge :
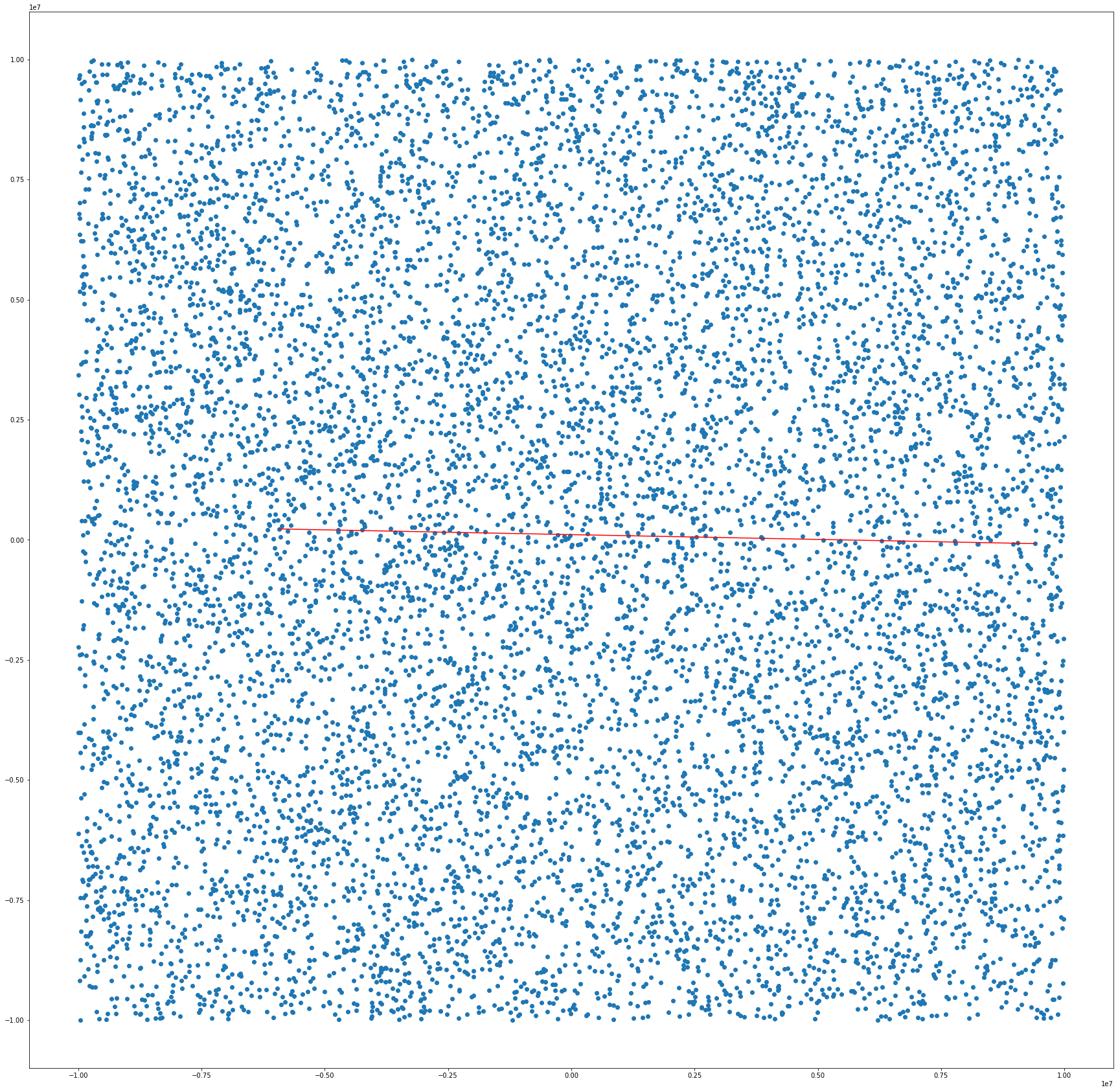
On peut aussi faire afficher les suites de points générées par le théorème en fonction du point de référence choisi au début des calculs. Voici les trajectoires que l’on obtient par exemple pour un ensemble de points :
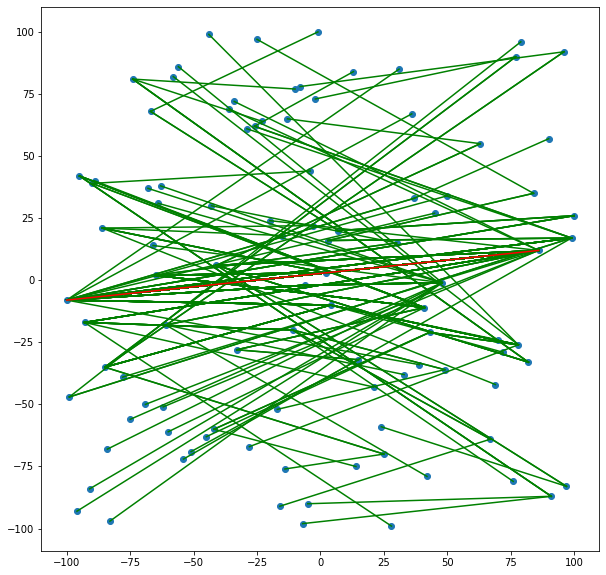
Il reste toutefois plusieurs conjectures à examiner :
– La suite de points que génère le théorème se termine toujours par une boucle sur un unique couple de points.
– La droite optimale trouvée est la plupart du temps unique sauf quelques cas pathologiques à définir.
– Lorsqu’il n’y a que deux points sur la droite optimale alors à un point près il y a autant de points au dessus de la droite qu’en dessous de la droite.
Ce problème n’a pas fini de révéler tous ses secrets. Les détails du théorème présenté dans cet article et sa preuve sont présentés dans le fichier joint ci-dessous.
