Le hasard au cœur de la matière - L'univers des mathématiques

Les mathématiques appliquées dans les sciences physiques nous donnent des équations qui nous permettent de prédire ensuite les résultats de diverses expériences sans même avoir à les réaliser. On peut finir par s’interroger ensuite si les expériences qui nous paraissent aléatoires ne le sont pas juste parce que nous n’avons pas encore découvert des équations capables de les prédire. Le hasard résulte-t-il simplement de notre absence de connaissance ou bien existe-t-il fondamentalement dans notre univers ? Cette question a longtemps divisé la communauté scientifique et opposé en 1927 deux brillants scientifiques : Niels Bohr et Albert Einstein. Une expérience récente réalisée depuis montre que le hasard semble exister bel et bien fondamentalement au cœur de la matière dans les particules élémentaires qui nous composent. Je vous propose d’illustrer cette expérience qui s’appuie sur les travaux du mathématicien John Bell dans une histoire fictive.

Nelson et Albus sont deux copains qui adorent jouer et faire toutes sortes d’expériences folles. Un jour Nelson appelle Albus pour lui montrer sa dernière découverte : un distributeur de balles magiques.

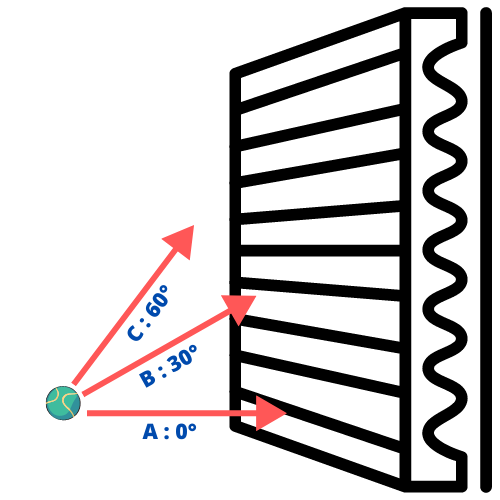
Nelson lui montre : « Regarde lorsque tu appuies sur le bouton de cette machine, tu récupères une balle magique. Elle est magique car lorsque tu la jettes en direction de ce filtre, elle réussit à passer au travers une fois sur deux ! En fait j’ai essayé de lancer des balles magiques de 3 façons différentes :
– Lancer de type $A$ : avec un angle de 0° par rapport au filtre.
– Lancer de type $B$ : avec un angle de 30° par rapport au filtre.
– Lancer de type $C$ : avec un angle de 60° par rapport au filtre.
Quelque soit le type de lancer que je choisis de reproduire 1000 fois, j’ai remarqué que environ 500 fois la balle magique traverse le filtre et que environ 500 fois elle ne le traverse pas ».

Trois différents lancers possibles d’une balle sur un filtre

Nelson continue ses explications : « Si on convient de noter $(+)$ l’évènement « la balle passe au travers du filtre » et $(-)$ l’évènement « la balle ne passe pas au travers du filtre » alors on peut considérer 6 évènements différents :
– $(A+)$ : « le lancer est de type A et la balle passe ».
– $(A-)$ : « le lancer est de type A et la balle ne passe pas ».
– $(B+)$ : « le lancer est de type B et la balle passe ».
– $(B-)$ : « le lancer est de type B et la balle ne passe pas ».
– $(C+)$ : « le lancer est de type C et la balle passe ».
– $(C-)$ : « le lancer est de type C et la balle ne passe pas ».
Je constate d’après mes expériences que la probabilité de chacun de ces évènements est de $1/2$ ! »

Albus répond à Nelson : « Je pense que dans le distributeur, on peut trouver simplement des balles qui ne passent jamais à travers le filtre et des balles qui traversent à coup sûr le filtre, de plus d’après tes expériences on peut affirmer qu’il y a autant de balles pour chacun de ces deux types dans le distributeur, voilà tout ! ».

Nelson rétorque : « Je pense plutôt que c’est au moment où la balle entre en contact avec le filtre que la décision de passer ou pas est prise. En effet, je ne t’ai pas tout raconté, j’ai remarqué que si je maintiens plus longuement le bouton de la machine il est possible d’obtenir deux balles en même temps et ces balles semblent liées d’une façon étrange :
– Si on lance les balles de la même façon (même type de lancer) alors elles ont des comportements identiques : elles passent toutes les deux ou elles ne passent pas toutes les deux.
– Si on lance les balles et que la différence d’angle entre les deux lancers est de 30° (lancers de types $A$ et $B$ ou lancers de types $B$ et $C$ ) alors elles ont des comportements identiques dans $3/4$ des cas et des comportements contraires dans $1/4$ des cas.
– Si on lance les balles et que la différence d’angle entre les deux lancers est de 60° (lancers de types $A$ et $C$ ) alors elles ont des comportements identiques dans $1/4$ des cas et des comportements contraires dans $3/4$ des cas. »

Nelson montre ensuite quelques dessins à Albus résumant les résultats de certaines expériences :

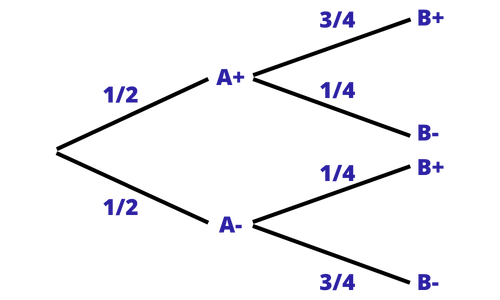
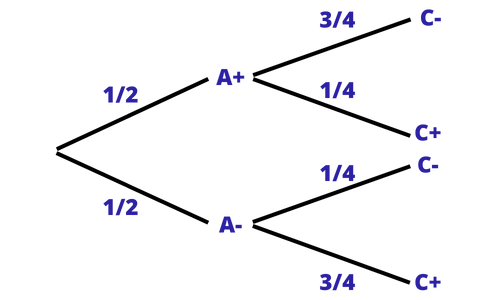
Deux lancers diffèrent de 30° : on peut remplacer A par C dans ce dessin

Nelson continue : « Lorsque le distributeur nous donne un couple de balles, c’est comme si chacune des deux balles était au courant du choix de l’autre. Tu peux même décider de faire un lancer de type $A$ sur un filtre qui se trouve en France puis de faire un lancer de type $B$ avec l’autre balle sur un filtre qui se trouve en Italie : le résultat du premier lancer influence celui du deuxième lancer ! »

Albus répond : « Ce que tu dis semble impossible : une action invisible à distance et instantanée. Voici une explication bien plus plausible : compte tenu de ce que tu me racontes, il n’y a pas deux types de balles dans le distributeur mais plutôt 8 types :
– Balle de type $A+\cap B+\cap C+$ : Cette balle passe à travers le filtre peu importe le type de lancer.
– Balle de type $A+\cap B+\cap C-$ : Cette balle passe à travers le filtre sauf si le lancer est de type $C$ .
– Balle de type $A+\cap B-\cap C+$ : Cette balle passe à travers le filtre sauf si le lancer est de type $B$ .
– Balle de type $A+\cap B-\cap C-$ : Cette balle ne passe pas à travers le filtre sauf si le lancer est de type $A$ .
– Balle de type $A-\cap B+\cap C+$ : Cette balle passe à travers le filtre sauf si le lancer est de type $A$ .
– Balle de type $A-\cap B+\cap C-$ : Cette balle ne passe pas à travers le filtre sauf si le lancer est de type $B$ .
– Balle de type $A-\cap B-\cap C+$ : Cette balle ne passe pas à travers le filtre sauf si le lancer est de type $C$ .
– Balle de type $A-\cap B-\cap C-$ : Cette balle ne passe pas à travers le filtre peu importe le type de lancer. »

Johnny un camarade de classe d’Albus et Nelson arrive et s’exclame : « Les copains, je vous écoutais depuis tout à l’heure et l’hypothèse d’Albus est en fait impossible pour une raison mathématique ». Johnny se met à écrire ses idées dans un cahier :

Supposons qu’il existe bien huit types de balles dans certaines proportions inconnues à l’intérieur du distributeur. On peut noter par exemple $\mathbb{P}(A+\cap B+)$ la proportion des balles dans le distributeur qui ont $(A+)$ et $(B+)$ dans leurs types. On a $\mathbb{P}(A+\cap B+)=\mathbb{P}(A+\cap B+\cap C+)+\mathbb{P}(A+\cap B+\cap C-)$ car les balles du distributeur sont forcément de type $C+$ ou de type $C-$ puis on obtient $\mathbb{P}(A+\cap B+)\leq \mathbb{P}(A+\cap C+)+\mathbb{P}(B+\cap C-)$ car on a les inclusions $(A+\cap B+\cap C+)\subset (A+\cap C+)$ et $(A+\cap B+\cap C-)\subset (B+\cap C-)$ . Cette inégalité n’est pas vérifiée d’après les expériences de Nelson puisque $\mathbb{P}(A+\cap B+)=1/2\times 3/4=3/8$ et $\mathbb{P}(A+\cap C+)+\mathbb{P}(B+\cap C-)=1/2\times 1/4+1/2\times 1/4=1/4=2/8$ . Comme cette inégalité n’est pas vérifiée on peut conclure que l’hypothèse de départ est fausse : les huit types de balles n’existent pas !

Ces expériences ont été faites en réalité par John Clauser et Alain Aspect qui ont reçu un prix Nobel en 2022 pour cela. Dans cette histoire, le distributeur de balles est un laboratoire de sciences, les balles magiques sont des photons et le filtre est un polariseur. Lorsque le distributeur de balles donne deux balles en même temps, il s’agit de photons intriqués. Existe-t-il une règle qui permet de prédire le comportement du photon devant un polariseur ? Cette règle ne dépend pas du polariseur car on peut affirmer avec certitude qu’un photon passe un polariseur lorsqu’on sait que son photon intriqué est déjà passé au travers d’un polariseur. Cette règle ne dépend pas aussi du photon car l’inégalité mathématique de John Bell n’est pas vérifiée expérimentalement. Nous devons envisager le cas où cette règle n’existe tout simplement pas : la décision du photon de passer ou de ne pas passer un polariseur serait alors totalement aléatoire !

Partager :

Laisser un commentaire Annuler la réponse