Le graphe d'une fonction continue - L'univers des mathématiques

Considérons une fonction $f$ définie sur un ensemble $A$ à valeurs dans $\mathbb{R}$ . Le graphe de $f$ sur $A$ est l’ensemble $G=\{ (x;f(x))\vert x\in A\}$ . Cet ensemble $G$ peut être représenté dans un repère du plan, voici par exemple ci-dessous la représentation du graphe (ou plus simplement représentation graphique) de la fonction $x\mapsto x^2$ sur $[-2;2]$ dans un repère orthonormé :

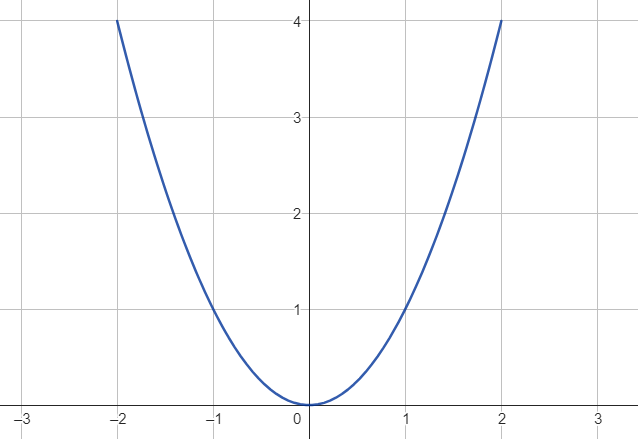
On s’intéresse dans cet article au graphe d’une fonction continue. Rappelons brièvement ce qu’est une fonction continue sur une partie $A$ d’un espace vectoriel normé. Soit $a \in A$ , la fonction $f$ est dite continue en un point $a$ si pour toute suite de nombres réels $u$ convergente vers $a$ la suite $f(u)$ est aussi convergente (on peut alors vérifier que la limite de $f(u)$ est forcément $f(a)$ ). On dit que $f$ est continue sur $A$ si $f$ est continue en tout point de $A$ . Cette définition est assez technique et abstraite ainsi on peut parfois entendre ou lire que le fait qu’une fonction est continue signifie simplement qu’il est possible de tracer sa représentation graphique sans lever le crayon ou encore que son graphe est en un seul morceau. Peut-on donner un sens précis à cette affirmation ? Cette affirmation est-elle d’ailleurs exacte et démontrée ? Voici les questions que l’on étudiera dans cet article.

La notion mathématique derrière l’idée d’un ensemble en un seul morceau est celle de la connexité. Dans l’étude des limites, les « morceaux » ou briques élémentaires de l’analyse sont les ensembles ouverts. Un élément $a$ d’un ensemble $A$ est dit à l’intérieur de $A$ lorsqu’on se retrouve dans l’ensemble $A$ en s’approchant suffisamment de $a$ . L’ensemble $A$ est dit ouvert si tous ses éléments sont à l’intérieur de $A$ . Par exemple $]-2;2[$ est ouvert tandis que $[-2;2[$ n’est pas ouvert puisque le nombre $-2$ n’est pas à l’intérieur de $[-2;2[$ . Maintenant que les ouverts sont définis on peut aller plus loin et dire qu’un ensemble $A$ n’est pas connexe lorsqu’il existe une partition de $A$ de la forme $\{X\cap A,Y\cap A\}$ avec $X$ et $Y$ des ouverts. Voici ci-dessous quelques ensembles connexes et non connexes du plan :

Pour décrire le fait d’être en un seul morceau, il y a une autre possibilité intéressante. Un ensemble $A$ est dit connexe par arcs si pour tout $(a,b)\in A^2$ il existe une fonction continue $\gamma$ définie sur $[0;1]$ à valeurs dans $A$ telle que $(\gamma(0);\gamma(1))=(a;b)$ . Intuitivement, cela veut dire que l’on peut relier deux points quelconques de notre ensemble $A$ par une courbe continue en restant dans l’ensemble $A$ . Quel est le lien entre la connexité et la connexité par arcs ? Le théorème ci-dessous montre que la différence est subtile :

Théorème : Soit $A$ une partie d’un espace vectoriel normé.
$A$ connexe $\implies A$ connexe par arcs
$(A$ ouvert et connexe par arcs $)\implies A$ connexe

Dans l’ensemble $\mathbb{R}$ les parties connexes et les parties connexes par arcs sont les mêmes : il s’agit des intervalles. Revenons à notre problème de départ : y a-t-il équivalence entre le fait d’affirmer qu’une fonction est continue sur un intervalle $I$ et le fait d’affirmer que son graphe est en un seul morceau ? La réponse dépend justement de ce que l’on convient d’appeler « être en un seul morceau ». Si cela nous évoque la notion de connexité alors on a le théorème suivant :

Théorème : Soit $I$ un intervalle et $f$ une fonction définie sur $I$ à valeurs dans $\mathbb{R}$ .
$f$ continue sur $I\implies$ Le graphe de $f$ sur $I$ est connexe

Toutefois la réciproque de ce dernier théorème est fausse et il n’y a donc pas d’équivalence ! Si le fait « d’être en un seul morceau » nous évoque plutôt la notion de connexité par arcs alors cette fois on dispose du théorème ci-dessous :

Théorème : Soit $I$ un intervalle et $f$ une fonction définie sur $I$ à valeurs dans $\mathbb{R}$ .
$f$ continue sur $I\iff$ Le graphe de $f$ sur $I$ est connexe par arcs

Les preuves des différents théorèmes et davantage de détails sont proposés dans le fichier joint ci-dessous.

Le graphe d’une fonction continue Télécharger

Partager :

Laisser un commentaire Annuler la réponse