Le centre d’un objet

Quel est le centre du triangle dessiné ci-dessous ?

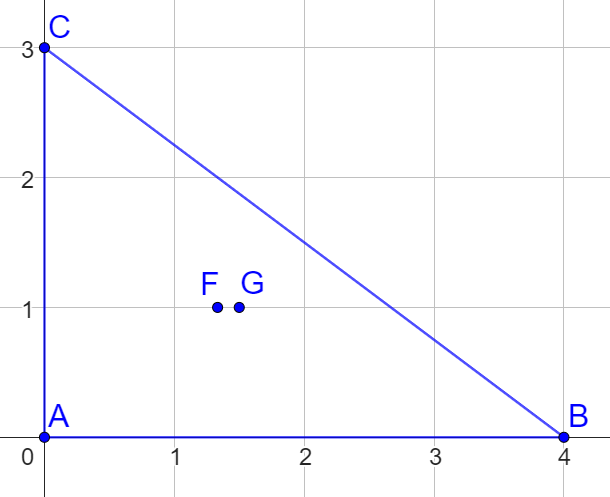
Pour répondre correctement à cette question, il convient en fait de préciser si l’on cherche le centre de la surface triangulaire ou le centre du contour triangulaire ! Si le triangle représente une plaque de matière homogène d’épaisseur constante alors le point est l’endroit où il faut positionner son doigt pour que la plaque puisse tenir en équilibre au dessus. On dit que est le centre de gravité de la plaque. Si le triangle représente cette fois un fil de matière homogène de diamètre constant alors son centre de gravité sera un point différent de ! Calculons ci-dessous les coordonnées de et de .

Pour calculer les coordonnées de , il nous suffit de calculer la moyenne des coordonnées des trois sommets et . Dans notre exemple on a et donc la somme des coordonnées est puis en divisant par on obtient .

Pour calculer les coordonnées de , il nous faut préalablement calculer les coordonnées des milieux de chaque côté ainsi que les longueurs de chaque côté :

– Le milieu de a pour coordonnées et on a .
– Le milieu de a pour coordonnées et on a .
– Le milieu de a pour coordonnées et on a .

Les coordonnées de sont obtenues en calculant la moyenne des coordonnées des milieux pondérée par les longueurs correspondantes ainsi l’abscisse de est . De même l’ordonnée de est et on obtient donc .

Peut-on résoudre le même problème si le segment est remplacé par le graphique d’une fonction quelconque, comme par exemple un arc de parabole ? De manière plus générale, comment peut-on calculer les coordonnées du centre d’une surface ou d’un contour quelconque ? Ces questions sont développées dans le fichier joint ci-dessous.